Maths & Musique #5: Musical temperament revisited, by Laurent Mazliak

The tonal system on which Western music has been based for centuries. The question of musical temperament has long permeated the history of Western music, arising from a very practical problem: how to tune a keyboard instrument (positives, organs, harpsichords, piano, etc.). The most emblematic and famous example is undoubtedly provided by Johann Sebastian Bach and his “ Well-Tempered Keyboard ”, a theoretical work in which the German composer sought to illustrate how the right choice of temperament for the keyboard could enable a satisfactory flow between the different major and minor keys.

Let's review some of the basics of this problem, then comment on the highly original use of temperament proposed by contemporary Hungarian composer György Ligeti in the first movement of his sonata for solo viola.

Consider a guitar string. The sound it emits when plucked is a periodic vibration of the air at a frequency f. In fact, scientists of the 17th and 18th centuries (notably Mersenne and d'Alembert) showed that this vibration is the juxtaposition of an infinite number of vibrations (known as harmonics) whose vibration frequencies are integer multiples of f : 2f, 3f, 4f etc. We also know that the frequency of the sound emitted is inversely proportional to the length of the string: for example, if you put your finger in the middle of the string, you'll get a note with a frequency of 2f ; if you put it at 1/3 of the length, you'll let 2/3 of the string vibrate, and you'll get a note with a frequency of 3/2f, etc.

The vibration of frequency 2f “matches” the vibration of frequency f very well, since the brain perceives these two sounds as being very close: they are said to be an octave apart, and the corresponding musical notes are given the same name. The next vibration is that of frequency 3f. As 3f = 2. (3/2 f), we can see that the corresponding note is the same as that of frequency 3/2.f : it's called the (ascending) fifth.

Starting with a sound of frequency f, by multiplying the frequency each time by 3/2, we can build a sequence of sounds separated from each other by an ascending fifth:

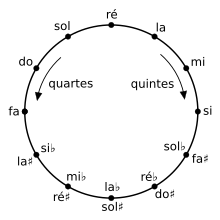
This construction (known as the cycle of fifths) a priori contains an infinite number of sounds, none of which is one or more octaves away from another, since no power of 3 equals a power of 2. But something interesting happens, because (3/2)¹² = 129.74... is rather close to²⁷ = 128. If we “pretend” that the two notes of frequency (3/2)¹² f and²⁷f are identical, we can put E# = F. One consequence of this is that the cycle of fifths closes, and we can consider the set of twelve notes constructed above (referred to as the chromatic total) as a closed set for the passage from fifth to fifth. Looking at the twelve notes constructed, we show that we can divide their frequency by a suitable power of 2 to obtain a frequency between f and 2fand obtain the following order:

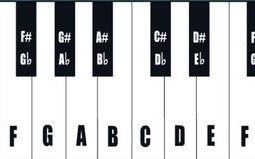
These twelve notes form the frieze that will be repeated from octave to octave on a keyboard instrument.

But we cheated by considering (3/2)¹² and²⁷ to be equal, and we'll have to take this error into account when tuning these twelve tones. One option is to distribute the error evenly over the 12 intervals, known as equal temperament. But this choice is totally artificial: the “natural” fifth ratios have simply disappeared, so that, so to speak, everything sounds (a little) wrong... In fact, there are infinite possibilities for tuners to distribute the error.

The question of musical temperament is only really crucial for keyboard instruments. On an instrument like the violin, the musician can place his or her finger on the string in places other than half, third, quarter... With great originality, Ligeti revisited the question on an instrument without a keyboard: a viola. To give the first movement Hora Lunga of his sonata for solo viola an atmosphere reminiscent of Transylvanian folk music, Ligeti invented a system of sound distribution based on frequency deviations from equal temperament.

Let's imagine a string with a fundamental frequency of F. By touching the string at specific points with his finger, the performer can play harmonics whose frequency is more or less deviated from the frequency obtained in equal temperament. However, a major difficulty arises: there is no F string on a viola. As a result, Ligeti asked the performer to perform a tour de force: in the first half of the piece, he had to copy the distribution of the different notes on the C string (on which the whole piece was to be played), with deviations corresponding to those of the fictitious F string. Ligeti therefore indicates on the score the notes on which to make deviations (measured in cents):

To achieve these notes, the violist must use a variety of methods, which can be mixed and matched:

• tune the viola's G string a tone higher, so that it produces an F, and listen to its natural harmonics;
   
• produce artificial harmonics by pressing the string firmly down on the desired fundamental note with one finger (similar to the capo principle on a guitar) and stroking the accessible nodes with the other finger of the same hand. On an instrument like a viola, depending on the size of their hand, performers can use this technique to reproduce notes from the second harmonic upwards. But notes above the 5th harmonic are almost impossible to sound;
   
• transpose (by imitating deviations) onto the F scale the sound of natural harmonics heard on another string;
   
• use a third person to make the harmonics sound by touching the string, while the performer keeps the fundamental pressed down (or vice versa).