Au coeur des nombres : représentations décimales et changements de base

Les représentations décimales ou binaires des nombres réels offrent certains avantages évidents : en représentant tous les nombres réels de façon uniforme, elles permettent d’effectuer mécaniquement et efficacement les opérations fondamentales de l’arithmétique (additions, soustractions, multiplications, divisions, etc.) et facilitent les comparaisons numériques. Savoir si un nombre est plus grand qu’un autre peut s’avérer bien utile ! Certaines approximations comme π  ≅ 3.14 font ainsi partie de la culture générale et nous manipul(i)ons1  quotidiennement des nombres entiers ou rationnels sous forme décimale.

Cette familiarité rend d’autant plus surprenant le profond mystère qui entoure ces représentations dès que les mathématicien.ne.s portent leur regard vers l’infini. En effet, bien que les deux énoncés :

Le chiffre 7 apparaît infiniment souvent dans le développement décimal de $\sqrt{2}$

et  

Votre numéro de carte bleue apparaît dans le développement décimal de $2^{n}$ dès que l’entier n est assez grand

soient très certainement vrais, leur démonstration semble à ce jour hors de portée; et l’on pourrait multiplier de tels exemples à l’envie, aussi simples à formuler qu’insaisissables. Ils reposent sur deux principes heuristiques fondamentaux :

1. les développements des nombres irrationnels apparaissant classiquement dans les manuels de mathématiques, comme $\sqrt{2}$ et π, sont complexes et n’obéissent à aucune régularité apparente.
2. un nombre réel (ou un ensemble d’entiers) ne peut pas avoir des représentations simples dans deux bases multiplicativement indépendantes (comme 2 et 10), sauf s’il est rationnel ou si l’ensemble d’entiers est périodique (union finie de progressions arithmétiques).

Le langage des probabilités, celui des systèmes dynamiques, ou encore celui de l’informatique ont été mobilisés pour formaliser ces intuitions, notamment par des mathématiciens de renom comme É. Borel [4], Morse et Hedlund, Furstenberg [5], Turing, Hartmanis et Stearns [6]. Inspiré par les travaux de ces derniers, Cobham a proposé, à la fin des années 1960, d’utiliser les automates finis [3] –machines de Turing très rudimentaires– pour définir une classe de nombres réels (et d’ensembles d’entiers) particulièrement simples. Un nombre réel est automatique relativement à la base entière b, si son développement en base b peut être calculé par une telle machine, et il existe une définition similaire pour les ensembles d’entiers. En 1969, Cobham a démontré un théorème remarquable : si un ensemble d’entiers est automatique relativement à deux bases multiplicativement indépendantes, alors il est nécessairement périodique.

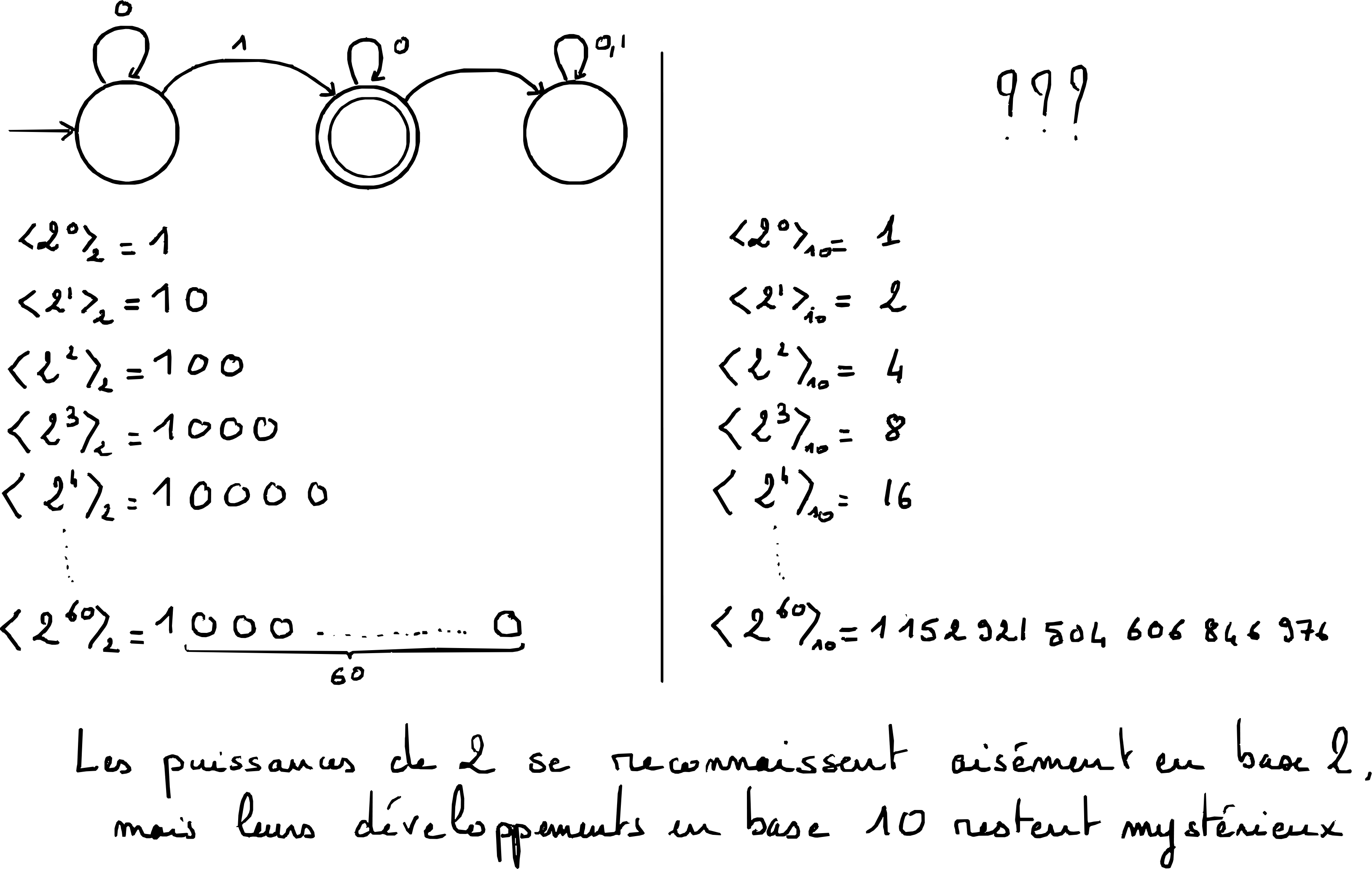
Dans l’esprit du premier principe, il a de plus conjecturé que le développement d’un nombre réel algébrique irrationnel, comme $\sqrt{2}$, n’est jamais automatique. Ce résultat a été prouvé plusieurs décennies plus tard par Adamczewski et Bugeaud [1], en s’appuyant sur un résultat diophantien profond : la version p-adique du théorème du sous-espace de Schmidt. Dans l’esprit du second principe, une autre conjecture naturelle, également conséquence d’une célèbre conjecture de Furstenberg [5], a ensuite émergé :

Un nombre réel qui est automatique dans deux bases multiplicativement indépendantes est nécessairement rationnel.

Cette conjecture a été récemment démontrée par Adamczewski et Faverjon [2], qui ont aussi donné une nouvelle preuve des théorèmes de Cobham et d’Adamczewski–Bugeaud, tout en les généralisant. Au-delà des résultats eux-mêmes, c’est le principe de démonstration qui mérite l’attention : il repose sur le développement d’une méthode introduite par Mahler à la fin des années 1920 pour démontrer la transcendance et l’indépendance algébrique de valeurs aux points algébriques de fonctions analytiques (d’une ou plusieurs variables) satisfaisant à un certain type d’équations fonctionnelles. Le fait que des méthodes issues de la transcendance puissent s’appliquer à d’autres domaines n’est pas nouveau. On pense naturellement aux problèmes de géométrie antique comme l’impossibilité de la quadrature du cercle (théorème de Lindemann), à la géométrie diophantienne (théorème de Siegel), ou encore à la théorie algébrique des nombres (théorème de Baker). Les travaux d’Adamczewski et Faverjon s’inscrivent dans cette grande tradition, enrichissant une liste déjà bien fournie de problèmes résolus à l’aide de méthodes transcendantes. 

• 1L’utilisation des parenthèses est un clin d’oeil à la disparition progressive du paiement en espèces, mais ce dernier n’est pas l’unique source de calcul dans la vie quotidienne.