The work of Hugo Duminil-Copin

1. Overview

Magnetism

Ice melts, water boils - these are examples of « phase transitions ». A further phase transition was studied experimentally by Pierre Curie for his 1895 Doctoral Thesis. A magnetized bar of iron retains its magnetization if and only if the temperature $T$  is sufficiently low, or more specifically $T< T_c$ for a critical temperature $T_c$ now termed  the « Curie point ». (In the case of iron, we have $T_c\approx 770^\circ$C.)

Spatial disorder

Gas particles are filtered through a disordered material. On a microscopic scale, the medium comprises fissures some but not all of which are wide enough to allow the gas to pass. The practical question is whether or not the gas passes through the filter.

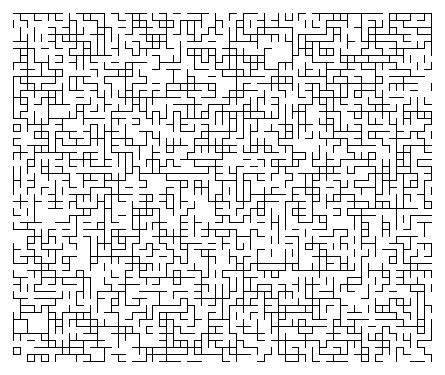
Mathematicians and theoretical physicists study such systems by building and analysing conceptual models. The fundamental models for magnetism and spatial disorder are, \resp, the « Ising model » (of 1920) and the « percolation model » (of 1957). See Figures \ref{fig:ising} and \ref{fig:perc}. These two models coexist within a large (and growing) family of models for disorder in physical systems. Together with their cousins, they have attracted an enormous amount of attention from mathematicians and physicists. Each model possesses a phase transition, and the principal challenges lie in understanding the nature of this transition. The mathematics of such systems is ramified, highly technical, and  very complex. Many significant problems have been overcome, and many remain. For example, the Ising model in two dimensions is now largely understood by mathematicians, whereas physicists are well ahead of mathematicians in three dimensions.

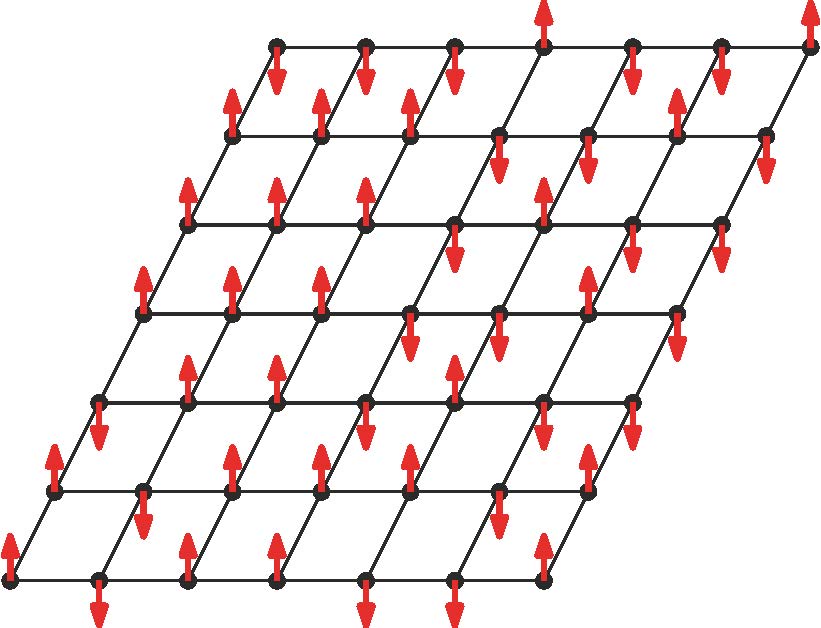
In recent years, no-one has advanced the mathematical theory of these and related systems more than Hugo Duminil-Copin. Hugo is an extraordinary mathematician who has achieved enormous progress. His many contributions to the theory of critical phenomena have resolved longstanding problems of deep significance, and have opened new directions of research.

From his 2011 PhD thesis onwards, Hugo Duminil-Copin has had unique impact on the rigorous theory. In a  large number of publications characterized by both depth and breadth, he has solved a wide range of important problems, and has introduced novelty and clarity to the methodology. At the same time, he has displayed outstanding qualities of leadership through his mentoring of early-career researchers.

Hugo Duminil-Copin's early work was based largely around the idea that critical systems in two dimensions are invariant under so-called « conformal mappings »; these are the mappings that are composed of local dilations and rotations. This topic has seen an explosion of progress over the last twenty years, starting with Oded Schramm's introduction of a type of random curve termed SLE. While still in his twenties, Hugo Duminil-Copin made several fundamental contributions, including rigorous derivations of long-conjectured critical probabilities and connective constants.

The hypothesis of « universality » asserts in such contexts that the nature of a phase transition depends only on the type of model and the number of dimensions; thus, for example, the phase transitions of percolation on the square and triangular  lattices are expected to be of common type. Hugo Duminil-Copin expanded his research interests to the study of universality in statistical physics, where he obtained a number of outstanding results, including the scaling relations for certain random-cluster models that incorporate both Ising and percolation models, together with fractal properties of continuous phase transitions.

Moving beyond two dimensions, Hugo Duminil-Copin has devised new methods to resolve a number of long-open and notorious classical problems in critical phenomena, including: (i) the continuity of the phase transition of the three-dimensional Ising model, (ii) the « triviality » of the Ising model scaling limits in four dimensions, and (iii) the sharpness of the phase transition for a range of stochastic models in arbitrary dimension. He has also made many significant and universal advances in the theory of off-critical phases of a number of statistical physics models of importance.

In the following sections, we describe in more detail  a selection of Duminil-Copin's profound and diverse contributions. For summaries of some of his results, the reader may consult his expository work [7, 8, 9, 10, 11, 12].

Most of Hugo's papers have been written jointly with others. He is invariably enthusiastic to share his ideas openly, and he collaborates freely and intensively with an unusually wide spread of colleagues, both younger and older. This practice has greatly augmented and amplified his beneficial impact on science.

2. Percolation, Ising, Potts models

The random-cluster model was introduced by Fortuin and Kasteleyn around 1970 as a unification of electrical networks, percolation, and the Ising/Potts models. It has become a focus of unification in the theories of these topics.

It was long conjectured that the critical point of the random-cluster model on the square lattice with cluster-weight $q$ is the self-dual point
$$
p_c(q) = \frac{\sqrt q}{1+\sqrt q}.
$$
The $q=1$ case is a famous result of Harris and Kesten (1980) for percolation, and the $q=2$ case amounts to an Onsager calculation (1944) for the Ising model. Some progress had been made by others for certain ranges of $q$, but the general result remained open until proved in 2012 by Duminil [4] (with Beffara). Their solution resolved, in particular, the (longstanding) conjectured value of the critical point  of the $q$-state Potts model on the square lattice.

In a subsequent work, [24], to which we return later, he introduced a new method for proving exponential decay (and more), and applied it to a spectrum of processes including all random-cluster models and Potts models. This has proved a major step towards a systematic theory of disordered systems.

Duminil-Copin has been instrumental in extending many of the classical percolation techniques from Bernoulli percolation (independent) models to a much wider class of dependent models.
With Hongler and Nolin [18], and later Chelkak and Hongler [6], he proved RSW-type a priori bounds for probabilities of crossings in the FK Ising model. This was an early example of an RSW-type theory for percolation models withdependence, and it paved the way to many later advances by Duminil-Copin and other authors.

Much attention has been given in the physics literature to the question of (dis)continuity in the phase transition of the two-dimensional Potts model. This was resolved by Hugo Duminil-Copin in [13] (with Gagnebin, Harel, Manolescu, Tassion) with the proof of discontinuity when $q>4$, and in [25] (with Sidoravicius and Tassion) with continuity when $1\le q \le 4$.
 

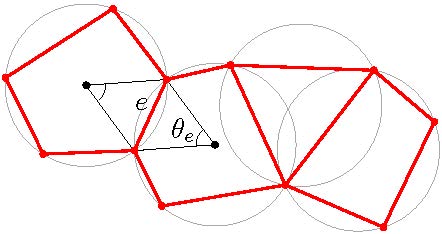
In two outstanding recent papers, with Li and Manolescu [21] and Manolescu [22], Hugo Duminil-Copin has proved certain scaling properties of random-cluster models. The first paper concerns isoradial graphs, as illustrated in Figure 3. Isoradiality enables the identification of the canonical critical points predicted by the star-triangle transformation (or Yang-Baxter relation); by judicious use of the star-triangle transformation, certain scaling properties may be propagated across the family of critical isoradial processes.The second paper establishes scaling relations for the critical model on the square lattice. Such results were known before only in the percolation case $q=1$ in famous work of Kesten. This pair of papers solve several big open problems, and constitute key progress towards proving universality for random-cluster models on isoradial graphs.

One of Duminil-Copin's recent results in this area is the striking proof [19] (joint with Kozlowski, Krachun, Manolescu, Oulamara) that the model on the square lattice with parameter $q\in [1,4]$ exhibits rotational invariance at large scales. The proof is a beautiful and technically demanding combination of several methods, including modification of the lattice by star-triangle transformations and Bethe ansatz calculations. This impressive development opens the way to promising approaches for proving full conformal invariance.

3. Self-avoiding walks

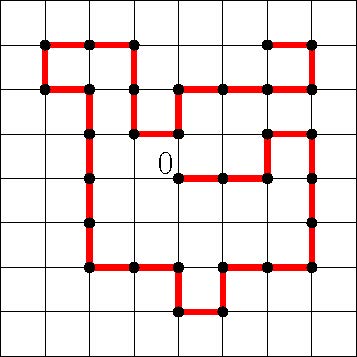
The theory of self-avoiding walks  (SAWs) offers perhaps some of the most challenging open problems in probability and combinatorial theory. (See Figure 4.) Hugo Duminil-Copin provided a startling solution to a notorious conjecture that emerged in 1982 work of Nienhuis in conformal field theory. He proved in [26] (joint with Smirnov) that the number of $n$-step self-avoiding walks on the hexagonal lattice grows in the manner of $\mu^{n+o(n)}$ with $\mu = \sqrt {2 + \sqrt {2}}$. The elegant proof uses a parafermionic observable (similar to the holomorphic observable used by Chelkak and Smirnov in the context of the Ising model), together with some neat counting/convergence arguments.

He has obtained a number of other important results about SAWs. Firstly, he showed in [17] (with Hammond) that SAW in dimensions $2$ and more are sub-ballistic; this may be viewed as the first non-trivial result in this direction for the « difficult » dimensions 2 and 3. Secondly, in the other direction his papers [14] (with Glazman, Hammond and Manolescu) concerning delocalization, and [20] (with Kozma and Yadin) concerning the space-filling property of supercritical SAW, are notable.

4. Ising and $\phi^4_4$ lattice models

Hugo Duminil-Copin has addressed several classical problems of critical phenomena which first achieved prominence in the 1980s. He began this project by identifying a list of fundamental challenges, being typically fundamental questions which were still viewed as being out of reach. He then achieved these goals in sequence. In some cases this was done via bold enhancements of known methods, and in others through the introduction of new ideas.

He showed in [2, 9] (with Aizenman and Sidoravicius) how to develop the random-current representation of the Ising model to resolve the problem of proving the continuity of the Ising phase transition in three dimensions. This is perhaps the first such result for any classical system in three dimensions, and it completes the picture for the Ising model in general dimensions. The proof techniques have since been utilized by several colleagues.

In the paper [1] (with Aizenman), Duminil-Copin showed the « marginal triviality » of the scaling limits of Ising and $\phi^4_4$ lattice models in four dimensions. Namely, the scaling limits of (near-)critical Ising and $\phi^4_4$ models are trivial (or Gaussian) as Euclidean field theories. Such triviality was derived in dimensions $d \ge5$ by Aizenman and Fröhlich (independently) in 1981/82. The recent extension to the (critical) dimension $d=4$  was obtained via a singular correction to previously deployed bounds. The last was derived through a multiscale analysis of the random-current intersection probability at the threshold dimension 4.

5. Sharpness of phase transitions

A major thrust of Duminil-Copin's work has been to understand the sub- and supercritical phases of models of statistical physics. There are classical methods that allow study of small and large parameter-values, but it is very much harder to study the phases right to the critical point. Hugo Duminil-Copin has many influential results in this direction, beginning with his proof of the critical point of the two-dimensional random-cluster model, [4].

In [24], Hugo Duminil-Copin (with Raoufi and Tassion) developed a beautiful method to prove exponential decay in the subcritical phase, therein making use of an inequality on decision trees of O'Donnell et al. The authors explained, in particular, how to use this for random-cluster models in all dimensions. This last result, which was previously known only when either $q=1$ or $q$ is sufficiently large, answers a problem of about 30 years standing. The method has many other novel applications, including the best proof of exponential decay for Voronoi percolation, [23]. For a two-dimensional system with a property of duality, it leads to the coincidence of the self-dual point and the critical point. This work has changed our vision of the property of so-called « sharp threshold ».  

One important and topical application of the above method is given in [16] (with Goswami, Rodriguez and Severo), where Hugo Duminil-Copin has studied phase transition for the $h$-level set of the Gaussian free field in dimension $\geq 3$, and has proved the sharpness of the critical value of $h$.

6. Further work

Hugo has a number of outstanding contributions that do not fit easily into the above classification, of which a few examples are mentioned here.

He established in [3] the sharp threshold for bootstrap percolation in all dimensions (with Balogh, Bollobás and Morris).

In [15] (with Goswami, Raoufi, Severo and Yadin), he established the Benjamini-Schramm conjecture that Bernoulli percolation on a Cayley graph with superlinear growth has $p_c<1$. This was achieved by exploiting a new connection between percolation and the Gaussian free field, which relates the connectivity properties of percolation clusters to the geometry of the graph.

Paper [5] (with Benjamini, Kozma and Yadin) is an interesting work on the dimension of spaces of harmonic functions on certain random graphs. This issue is connected with a number of other topics including the theory of  random walks in random environments.

7. Summary

Hugo Duminil-Copin has found new ways of looking at old problems. He has obtained solutions to classical problems of great visibility, while simultaneously introducing new methods and intuitions into the field. His area of mathematical science has been largely reshaped by his achievements.

Hugo displays the strongest personal attributes in addition to his scientific talent. The fact that almost all his papers are in collaboration reflects his desire to communicate with and to excite others, and he invariably succeeds.    

Acknowledgements

The author acknowledges the contributions of several colleagues to this scientific biography. The photograph is included with the kind permission of IHES.