Les travaux d'Hugo Duminil-Copin

1. Contexte

Magnétisme

La glace fond, l'eau bout - ce sont des exemples de "transitions de phase". Une autre transition de phase a été étudiée expérimentalement par Pierre Curie pour sa thèse de doctorat en 1895. Une barre de fer magnétisée conserve son aimantation si et seulement si la température $T$ est suffisamment basse, ou plus précisément $T< T_c$ pour une température critique $T_c$ maintenant appelée "point de Curie". (Dans le cas du fer, nous avons $T_c\approx 770^\circ$C.)

Désordre spatial

Des particules de gaz sont filtrées à travers un matériau désordonné. À l'échelle microscopique, le milieu comporte des fissures dont certaines, mais pas toutes sont suffisamment larges pour permettre le passage du gaz. La question pratique est de savoir si le gaz passe ou non à travers le filtre.

Les mathématiciennes et mathématiciens, les physiciennes et physiciens théoriques étudient ces systèmes en construisant et en analysant des modèles conceptuels. Les modèles fondamentaux pour le magnétisme et le désordre spatial sont, par exemple, le "modèle d'Ising" (de 1920) et la "percolation" (de 1957). Voir les figures 1 et 2. Ces deux modèles coexistent au sein d'une grande famille (en pleine expansion) de modèles du désordre dans les systèmes physiques. Avec leurs cousins, ils ont attiré une attention considérable en mathématiques et en physique. Chaque modèle possède une transition de phase, et les principaux défis consistent à comprendre la nature de cette transition. Les mathématiques de ces systèmes sont ramifiées, très techniques et très complexes. De nombreux problèmes importants ont été résolus, et beaucoup restent à résoudre. Par exemple le modèle d'Ising en deux dimensions est maintenant largement compris en mathématiques,  alors que la physique est  très en avance sur les mathématiques en trois dimensions.

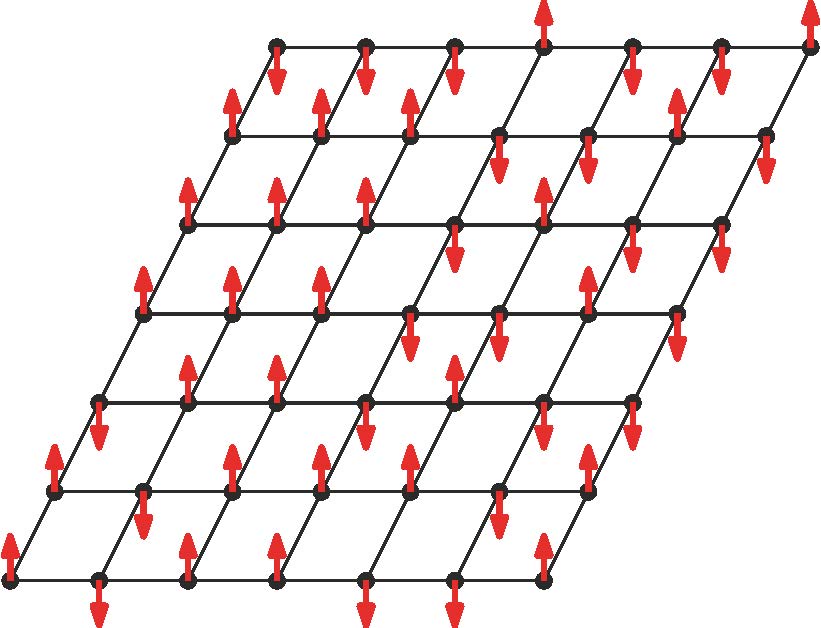
Ces dernières années, personne n'a autant fait progresser la théorie mathématique de ces systèmes et des systèmes connexes que Hugo Duminil-Copin. Hugo est un mathématicien extraordinaire qui a réalisé d'énormes progrès. Ses nombreuses contributions à la théorie des phénomènes critiques ont permis de répondre à des questions posées de longue date et d'une grande importance, et ont ouvert de nouvelles voies de recherche.

Depuis sa thèse de doctorat en 2011, Duminil-Copin a eu un impact unique sur la théorie rigoureuse de ces modèles. Dans un grand nombre de publications caractérisées à la fois par leur profondeur et leur ampleur, il a résolu un large éventail de problèmes importants, et a introduit de la nouveauté et de la clarté dans la méthodologie. Dans le même temps, il a fait preuve de qualités exceptionnelles de leadership en encadrant des chercheurs en début de carrière.

Les premiers travaux de Duminil-Copin reposaient en grande partie sur l'idée que les systèmes critiques en deux dimensions sont invariants (à grande échelle) sous l'effet de ce que l'on appelle les "applications conformes" ; il s'agit des applications qui sont composées de dilatations et de rotations locales. Ce sujet a connu des progrès fulgurants au cours des vingt dernières années, à commencer par l'introduction par Oded Schramm d'un type de courbe aléatoire appelé SLE. Alors qu'il était encore âgé de moins de trente ans, Duminil-Copin a apporté plusieurs contributions fondamentales, notamment des calculs rigoureux de paramètres critiques et de constantes de connectivité conjecturées depuis longtemps.

L'hypothèse d'"universalité" affirme dans de tels contextes que la nature d'une transition de phase ne dépend que du type de modèle et du nombre de dimensions ; ainsi, par exemple, les transitions de phase de la percolation sur les réseaux carrés et triangulaires sont censées être de même type. Duminil-Copin a étendu ses intérêts de recherche à l'étude de l'universalité en physique statistique, où il a obtenu un certain nombre de résultats remarquables, notamment les "relations de scaling" entre exposants critiques pour certains modèles de precolation dépendante qui intègrent à la fois les modèles d'Ising et de percolation, ainsi que des propriétés fractales des transitions de phase continues.

Au-delà de deux dimensions, Duminil-Copin a conçu de nouvelles méthodes pour résoudre un certain nombre de problèmes classiques notoires et ouverts depuis longtemps dans le domaine des phénomènes critiques, notamment : (i) la continuité de la transition de phase du modèle d'Ising tridimensionnel, (ii) la trivialité des limites d'échelle du modèle d'Ising en quatre dimensions, et (iii) le fait que la transition de phase siot abrupte pour de nombreux modèles stochastiques en toute dimension. Il a également réalisé de nombreuses avancées significatives et universelles dans la compréhension en dehors du point critique d'un certain nombre de modèles importants de la physique statistique.

Dans les parties suivantes, nous décrivons plus en détail une sélection des contributions profondes et diverses de Duminil-Copin. Pour des résumés de certains de ses résultats, le lecteur peut consulter ses travaux d'exposition : [7, 8, 9, 10, 11, 12].

La plupart des articles d'Hugo ont été écrits en collaboration avec d'autres personnes. Il est invariablement enthousiaste à l'idée de partager ses idées ouvertement, et il collabore librement et intensivement avec un éventail inhabituellement large de collègues, jeunes ou plus âgés. Cette pratique a considérablement augmenté et amplifié son impact bénéfique sur la science.

2. Modèles de percolation, d'Ising et de Potts

Le "modèle d'amas aléatoire" (ou "FK-percolation", en anglais "random-cluster model") a été introduit par Fortuin et Kasteleyn vers 1970 comme une unification des réseaux électriques, de la percolation et des modèles d'Ising et de Potts. Il est devenu un point essentiel de l'unification des théories sur ces sujets.

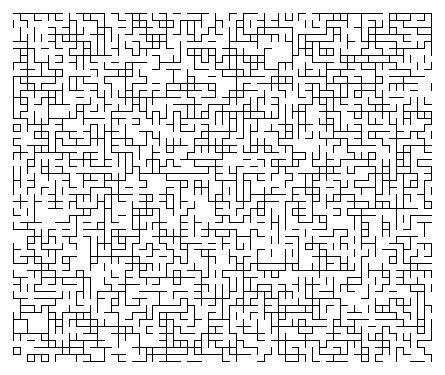
On a longtemps conjecturé que le point critique du modèle d'amas aléatoire sur le réseau carré avec un poids d'amas $q$ est le point auto-dual
$$
p_c(q) = \frac{\sqrt q}{1+\sqrt q}.
$$
Le cas $q=1$ est un résultat célèbre de Harris et Kesten (1980) pour la percolation, et le cas $q=2$ se ramène à un calcul d'Onsager (1944) pour le modèle d'Ising. Des progrès avaient été réalisés par d'autres pour certaines plages de $q$, mais le résultat général est resté ouvert jusqu'à ce qu'il soit prouvé en 2012 par Duminil [4] (avec Beffara). Leur solution a déterminé, en particulier, la valeur conjecturée (de longue date) du point critique du modèle de Potts à $q$ états sur le réseau carré.

Dans un travail ultérieur, [24], sur lequel nous reviendrons plus tard, il a introduit une nouvelle méthode pour prouver la décroissance exponentielle de fonctions de corrélation (et plus encore), et l'a appliquée à un ensemble de processus comprenant tous les modèles FK et les modèles de Potts. Cela a constitué une étape majeure vers une théorie systématique de ces systèmes désordonnés.

Duminil-Copin a joué un rôle déterminant dans l'extension de nombreuses techniques classiques dans le cas de la percolation de Bernoulli (indépendante) à une classe beaucoup plus large de modèles dépendants. Avec Hongler et Nolin [18], et plus tard Chelkak et Hongler [6], il a prouvé des bornes a priori de type RSW pour les probabilités de croisements dans le modèle FK Ising. Il s'agit d'un premier exemple de théorie de type RSW pour les modèles de percolation avec dépendance, qui a ouvert la voie à de nombreuses avancées ultérieures de Duminil-Copin et d'autres auteurs.

Une grande attention a été accordée dans la littérature physique à la question de la (dis)continuité de la transition de phase du modèle de Potts bidimensionnel. Cette question a été résolue par Duminil-Copin dans [13] (avec Gagnebin, Harel, Manolescu, Tassion) avec la preuve de la discontinuité lorsque $q>4$, et dans [25] (avec Sidoravicius et Tassion) avec la continuité lorsque $1\le q \le 4$.

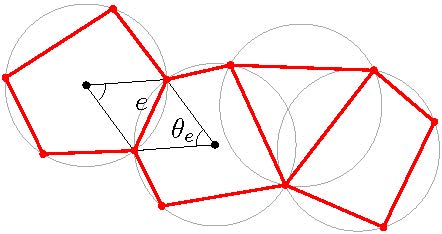
Dans deux articles récents remarquables, avec Li et Manolescu [21] et Manolescu [22], Duminil-Copin a prouvé certaines propriétés de scaling des modèles FK. Le premier article concerne les graphes isoradiaux (voir figure 3). L'isoradialité permet d'identifier des points critiques en exploitant la transformation triangle-étoile (ou relation de Yang-Baxter) ; par une utilisation judicieuse de la cette transformation, certaines propriétés d'échelle peuvent être propagées à toute une famille de processus critiques. Le second article établit des relations d'échelle pour le modèle critique sur le réseau carré. De tels résultats n'étaient connus auparavant que dans le cas de la percolation $q=1$ dans les célèbres travaux de Kesten. Ces deux articles résolvent plusieurs grands problèmes ouverts et constituent des progrès clés vers une preuve de l'universalité des modèles d'amas aléatoires sur les graphes isoradiaux.

Un des résultats récents de Duminil-Copin dans ce domaine est la preuve frappante [19] (conjointe avec Kozlowski, Krachun, Manolescu, Oulamara) que le modèle sur le réseau carré avec paramètre $q\in [1,4]$ présente une invariance par rotation à grande échelle. La preuve est une combinaison magnifique et techniquement exigeante de plusieurs méthodes, dont la modification du réseau par des transformations triangle-étoile et des calculs d'ansatz de Bethe. Ce développement impressionnant ouvre la voie à des approches prometteuses pour prouver l'invariance conforme complète.

3. Marches auto-évitantes

La théorie des marches auto-évitantes (MAE) offre peut-être certains des problèmes ouverts les plus stimulants de la théorie des probabilités et de la théorie combinatoire. (Voir la figure 4.) Duminil-Copin a fourni une solution étonnante à une conjecture notoire apparue en 1982 dans les travaux de Nienhuis en théorie des champs conformes. Il a prouvé dans [26] (conjointement avec Smirnov) que le nombre de marches auto-évitantes à $n$ pas sur le réseau hexagonal croît comme $\mu^{n+o(n)}$ avec $\mu = \sqrt {2 + \sqrt {2}}$. La preuve élégante utilise une observable parafermionique (similaire à l'observable holomorphe utilisée par Chelkak et Smirnov dans le contexte du modèle d'Ising), ainsi que quelques arguments fins de comptage et de convergence.

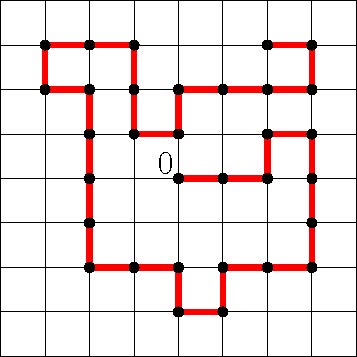
Il a obtenu un certain nombre d'autres résultats importants sur les MAE. Premièrement, il a montré dans [17] (avec Hammond) que les MAE en dimension $2$ et plus sont sous-ballistiques ; ceci peut être considéré comme le premier résultat non-trivial dans cette direction pour les dimensions "difficiles" 2 et 3. Deuxièmement, dans l'autre direction, ses articles [14] (avec Glazman, Hammond et Manolescu) concernant la délocalisation, et [20] (avec Kozma et Yadin) concernant la propriété de remplissage d'espace des SAW supercritiques, sont remarquables.

4. Modèle d'Ising et modèle $\phi^4_4$ sur réseau

Duminil-Copin s'est attaqué à plusieurs problèmes classiques de phénomènes critiques qui ont pris de l'importance dans les années 1980. Il a commencé ce projet en identifiant une liste de défis fondamentaux, à savoir des questions fondamentales représentatives qui étaient encore considérées comme hors de portée.  Il a ensuite atteint ces objectifs dans l'ordre.  Dans certains cas, cela s'est fait par des améliorations audacieuses de méthodes connues, et dans d'autres par l'introduction de nouvelles idées.

Il a montré dans [2, 9] (avec Aizenman et Sidoravicius) comment développer la représentation en courants aléatoires du modèle d'Ising pour résoudre le problème de la preuve de la continuité de la transition de phase d'Ising en trois dimensions. Il s'agit peut-être du premier résultat de ce type pour un système classique en trois dimensions, et il complète le tableau pour le modèle d'Ising en dimensions générales. Les techniques de preuve ont depuis été utilisées par plusieurs collègues.

Dans l'article [1] (avec Aizenman), Duminil-Copin a montré la "trivialité marginale" des limites d'échelle du modèle d'Ising et du modèle $\phi^4_4$ sur réseau en quatre dimensions. En d'autres termes, les limites d'échelle des modèles (quasi-)critiques d'Ising et de $\phi^4_4$ sont triviales (ou gaussiennes) en tant que théories des champs euclidiennes.  Cette trivialité avait été démontrée en dimensions $d \ge5$ par Aizenman et Fröhlich (indépendamment) en 1981/82. L'extension récente à la dimension (critique) $d=4$ a été obtenue par une correction singulière des limites précédemment déployées.  Cette dernière a été déduite d'une analyse multi-échelle de la probabilité d'intersection des courants aléatoires à la dimension seuil 4.

5. Transitions de phase abruptes

L'un des axes majeurs du travail de Duminil-Copin a été de comprendre les phases sous- et sur-critiques des modèles de physique statistique. Il existe des méthodes classiques qui permettent d'étudier les petites et grandes valeurs des paramètres, mais il est beaucoup plus difficile d'étudier ce qui se passe au voisinage du point critique. Duminil-Copin a obtenu de nombreux résultats influents dans cette direction, à commencer par sa preuve du point critique du modèle bidimensionnel d'amas aléatoires, [4].

Dans [24], Duminil-Copin (avec Raoufi et Tassion) a développé une belle méthode pour prouver la décroissance exponentielle dans la phase sous-critique, en utilisant une inégalité sur les arbres de décision de O'Donnell et al. Les auteurs ont expliqué, en particulier, comment l'utiliser pour les modèles d'amas aléatoires en toutes dimensions. Ce dernier résultat, qui n'était auparavant connu que lorsque soit $q=1$, soit $q$ est suffisamment grand, répond à un problème vieux d'environ 30 ans. La méthode a de nombreuses autres applications nouvelles, notamment la meilleure preuve de décroissance exponentielle pour la percolation de Voronoï, [23]. Pour un système bidimensionnel ayant une propriété de dualité, elle conduit à la coïncidence du point auto-dual et du point critique. Ce travail a changé notre vision de la propriété de "phénomène de seuil".

Une application importante et actuelle de la méthode ci-dessus est donnée dans [16] (avec Goswami, Rodriguez et Severo), où Duminil-Copin a étudié la transition de phase pour l'ensemble de niveau $h$ du champ libre Gaussien en dimension $\geq 3$, et a prouvé la "sharpness" de la valeur critique de $h$.

6. Autres travaux

Hugo a apporté un certain nombre de contributions remarquables qui ne rentrent pas facilement dans la classification ci-dessus, dont quelques exemples sont mentionnés ici.

Il a établi dans [3] le seuil exact de percolation bootstrap en toutes dimensions (avec Balogh, Bollobás et Morris).

Dans [15] (avec Goswami, Raoufi, Severo et Yadin), il a établi la conjecture de Benjamini-Schramm selon laquelle la percolation de Bernoulli sur un graphe de Cayley à croissance superlinéaire a $p_c<1$. Il y est parvenu en exploitant une nouvelle connexion entre la percolation et le champ libre Gaussien, qui relie les propriétés de connectivité des amas de percolation à la géométrie du graphe.

L'article [5] (avec Benjamini, Kozma et Yadin) est un travail intéressant sur la dimension des espaces de fonctions harmoniques sur certains graphes aléatoires. Cette question est liée à un certain nombre d'autres sujets, notamment la théorie des marches aléatoires dans des milieux aléatoires.

7. Résumé

Hugo Duminil-Copin a trouvé de nouvelles façons d'aborder de vieux problèmes. Il a obtenu des solutions à des problèmes classiques de grande visibilité, tout en introduisant simultanément de nouvelles méthodes et de nouvelles intuitions dans le domaine. Son domaine des mathématiques a été largement remodelé par ses réalisations.

En plus de son talent scientifique, Hugo fait preuve des plus grandes qualités personnelles. Le fait que presque tous ses articles sont en collaboration reflète son désir de communiquer avec les autres et de les enthousiasmer, et il y parvient invariablement.

Remerciements

L'auteur remercie plusieurs collègues pour leur contribution à cette biographie scientifique. La photographie est incluse avec permission de l'IHES.