Maths & Océans #2 : Mascaret, l’onde de marée

Aux grandes marées de septembre, le mascaret redevient d’actualité. Esquissons ici quelques éléments de description de cette vague remontant les fleuves, qui fascine toute la planète (voir les vidéos de foules de spectateurs en Chine (Hangzhou), parfois douchés par ces flots impressionnants).

L’origine du nom français reste a priori inconnue. Il est intéressant de noter qu’en gascon, le substantif « mascaret » qualifie les bœufs tachetés de noir, blanc et gris1 . Or, lorsqu’il déferle dans le fleuve, ce phénomène apparaît effectivement avec ces couleurs à la surface dues à l’écume et aux sédiments inévitablement présents (voir Figure 12 ). De plus, le bruit, se propageant loin à l’intérieur des terres, ressemble à s’y méprendre à celui d’un troupeau de bœufs au galop.

Il se dit souvent que le mascaret n’a lieu qu’une fois par an, à la grande marée de l’équinoxe de septembre. En fait, il peut se produire toute l’année mais l’onde n’est pas toujours observable « à l’œil nu » et la vague déferle assez fréquemment : environ 50 jours par an en Gironde, un lieu connu pour cela, qui nous sert de fil rouge dans ce texte.

Le phénomène s’observe en de nombreux endroits de la planète. En France, nous pouvons mentionner sa présence en Aquitaine, sur la Dordogne et la Garonne, en Normandie, au Mont-Saint-Michel, et en Picardie, dans la Baie de Somme.

À l’étranger, des mascarets célèbres sont : le Severn bore sur la Severn River au Royaume-Uni, le Guanchao sur la Qiantang en Chine, la Pororoca sur l’Amazone au Brésil. Et, mis sur le devant de la scène plus récemment, le Bono (surnommé les « sept fantômes ») sur l’île de Sumatra.

Le mascaret se forme au moment où le courant de marée montante, qui s’oppose au flux naturel du fleuve, se concentre et génère une onde dite « de marée », qui va remonter le cours d’eau sur des dizaines de kilomètres (par exemple, en Gironde, sur plus de 150 km et deux fois par jour). Cette onde peut, en fonction des conditions, déferler et créer une vague surfée par des passionnées et de passionnés : on parle alors de mascaret. Au niveau de l’embouchure, la forme du delta, sa largeur et sa pente sont des paramètres importants de la génération du mascaret. À l’intérieur des terres, la profondeur, la largeur du lit et les méandres vont également modifier la propagation et le déferlement comme pour une vague océanique. La vague peut disparaître et réapparaître avec les variations du fond.

On comprend donc qu’en modifiant la forme du fleuve3 , on puisse faire disparaître le déferlement du mascaret, pour éviter ses désagréments (destruction des berges, navigabilité, etc.). C’est ce qui a été réalisé notamment sur la Seine dans les années 1960, qui pouvait auparavant voir une vague de quatre mètres déferler sur toute sa largeur (comme le montrent des photos d’époque à Quillebeuf, par exemple)4 .

Figure 2 [photographies ci-dessous] : Le mascaret sur la Seine à Quillebeuf, au début du XXe siècle5 .

L’heure d’arrivée du mascaret est prévisible à quelques minutes près grâce à la connaissance des horaires de marée. Le coefficient de marée (>90 – 100, pour une belle onde en Gironde) donne une idée de sa taille. Elle peut toutefois être modifiée par le niveau d’eau dans le fleuve (qui varie en fonction des précipitations récentes).

Voici quelques ordres de grandeurs typiques (taille/vitesse) pour les mascarets évoqués précédemment (c’est tout à fait approximatif, cela dépend de l’évènement, et aussi, rappelez-vous que la taille et la vitesse varient le long du fleuve au cours de la propagation) :

• Dordogne : 1.5 m à une vitesse d’environ 15 km/h,

• Seine (avant l’ingénierie modifiant le fleuve) : 3 - 4 m à environ 20 km/h,

• Qiantang : 3 m en moyenne (parfois plus, lors de circonstances extrêmes) à environ 25 km/h,

• Pororoca : jusqu’à 4 m et 25 km/h.

Nous pouvons revenir sur le cas de la Gironde : dans son estuaire qui recueille la Garonne et la Dordogne, une vague peut se créer sur toute la largeur. Ne pouvant aller plus haut que l’onde de marée, le mascaret s’arrête vers Génissac sur la Dordogne et vers La Réole sur la Garonne. Le spot de surf le plus connu (et le plus médiatisé en France) est probablement à Saint-Pardon où se trouve une portion rectiligne de près de 5km. On compte, d’après la presse régionale, 3 à 4000 participantes et participants en septembre, mais pas toutes et tous dans l’eau !

Il nous semble également intéressant d’en dire un peu plus sur le Bono et les sept fantômes (voir Figure 36 ). Il s’agit d’un magnifique mascaret sur la Kampar River à Sumatra, où l’on peut voir très distinctement sur certains angles de vue, sept ondes en quinconce assez uniques (partiellement à l’origine du surnom). Typiquement, sa taille peut aller jusqu’à 2.5 m et sa vitesse est d’environ 20 km/h. Le Bono a été mis en lumière en 2011 par un explorateur du phénomène, Antony Colas7 , qui y a piloté une équipe de surfeuses et surfeurs professionnels. Ils ont ainsi produit des images, rares à cette époque, de tubes bien formés, à taille humaine et surfés sur un fleuve. Une superbe vidéo est disponible sur le lien suivant : Lien8 .

Quels sont les échos de la recherche mathématique en interaction avec la physique, sur les mascarets ?

Le phénomène fait toujours l’objet de recherches actives pour en comprendre les aspects fins, dont certains sont liés également à des questions plus abstraites.

Les mascarets sont associés à la transformation de l’onde de marée en un « ressaut hydraulique », un peu comme celui de l’évier de la cuisine [film]. Pour faire simple, il s’agit d’une vague avec une marche prononcée à l’avant, qui se propage à vitesse constante et sans changer de forme9 . Toutefois, et c’est relativement récent, on commence à enrichir la description de ce ressaut en ajoutant des effets dits dispersifs qui modifient la forme de l’onde10 .

Pour celles et ceux qui veulent aller plus loin, l’un des outils techniques utilisés pour décrire cette dispersion sont les équations de Serre Green-Naghdi11 . On peut toutefois donner l’intuition de façon accessible de ces effets dispersifs, avec le schéma suivant qui montre l’évolution de la forme de l’onde dans le temps et dans l’espace avec des grandeurs typiques. Deux courbes sont fournies : l’une avec un modèle sans dispersion (courbe noire, « très simple »), et l’autre avec un modèle contenant de la dispersion (courbe bleue, où des « oscillations » s’amplifient au cours du temps).

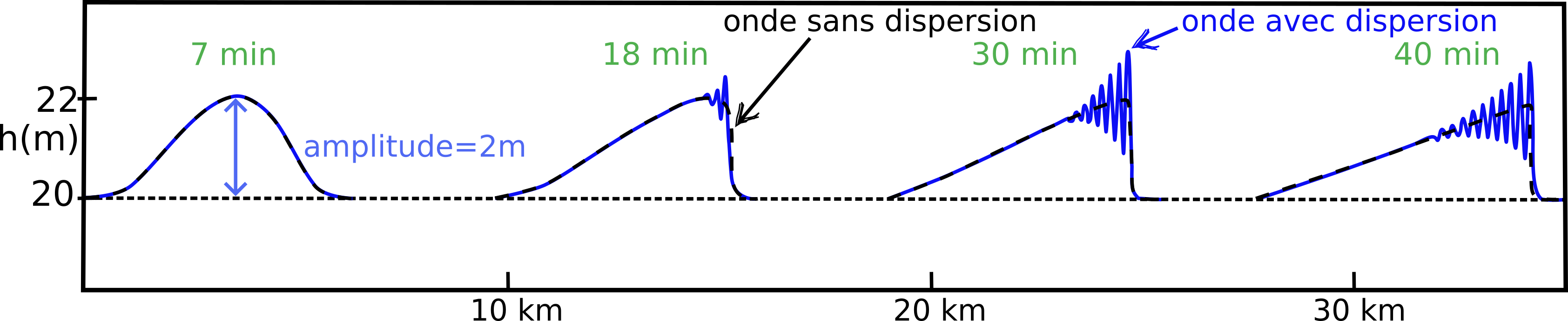
Pour l’anecdote bien réelle, les surfeuses et les surfeurs de mascaret reconnaîtront très vite le train d’onde dispersif subit dans la nature : si la vague avant vous dépasse, celles qui suivent derrière ne vous seront pas d’une grande utilité ! Le train s’éloignera sans vous, ce n’est malheureusement pas l’Ohana comme dans Lilo & Stitch !

Vous aurez aussi probablement remarqué que, pour les deux types de courbes, on observe un changement de pente des deux côtés de la vague. Notamment, la face avant de la vague tend vers une pente quasi verticale : cela fait l’objet de cours de mathématiques d’introduction sur le sujet (voir aussi ici la courbe bleue) mais également de recherches actuelles ardues (par exemple, en lien avec la question de la description du phénomène de déferlement de la vague, que ce soit en mer ou en rivière).

Pour obtenir la Figure 4, les scientifiques ont mélangé leurs expertises pour proposer un modèle adapté au mascaret et des méthodes numériques novatrices qui ont permis de donner de nouveaux éclairages sur ce phénomène. Les simulations ont mis par exemple en évidence l’influence du type de marée, du frottement au fond et de la forme de l’estuaire12 . Il est intéressant de noter aussi que l’étude des effets dispersifs ne concerne pas que le mascaret et l’hydrodynamique (les mathématiques produites pour ces questions de dispersion sont utilisées dans différentes disciplines). On la retrouve dans des domaines contemporains tels que les communications internet via les fibres optiques (propagation de la lumière sur de longues distance), les semi-conducteurs (smartphones et ordinateurs) ou encore les ondes dans les plasmas pour la fusion nucléaire.

Le mascaret est un phénomène pouvant être tour à tour magnifique et dangereux. Les mathématiques en interaction peuvent aider à améliorer la compréhension, la prédiction et la prévention de ce risque naturel. Cet exemple n’est qu’une illustration parmi tant d’autres du dialogue fructueux entre mathématiques et géophysique. Tenter de répondre à des questions de géophysique conduit à créer des problèmes mathématiques nouveaux et variés. Et réciproquement, les nouvelles méthodes mathématiques permettent d’obtenir des résultats plus précis et, souvent, de mieux comprendre la physique.

Remerciements

L'auteur souhaite remercier chaleureusement Philippe Bonneton pour ses exposés lumineux sur l'hydrodynamique côtière, depuis de longues années. Cet article lui doit beaucoup. Un grand merci également à Antony Colas pour nous avoir transmis les photos de mascaret en Gironde et à Sumatra.

• 1Dictionnaire du béarnais et du gascon modernes. Simin Palay. Editions CNRS, 1980
• 2YEP 2006. Podensac, en Gironde
• 3Construction de digues, modification des berges, dragages réguliers du fond à l’embouchure, etc.
• 4Il convient aussi de rappeler que le mascaret n’est pas à l’origine du décès sur la Seine de Léopoldine, fille de Victor Hugo ; les causes seraient plutôt un coup de vent et une embarcation mal équilibrée.
• 5E. Mellet, éditeur de cartes postales à Harfleur (Seine-Maritime). Années 1920 (1927 ?) ; L ' Hernault, éditeur de cartes postales au Havre (Normandie). Date inconnue mais avant 1963.
• 6 YEP, Rip Curl, Nate Lawrence, 2011 Bono campaign
• 7Mascaret, prodige de la marée. Antony Colas, YEP editions, Novembre 2017.
• 8 YouTube/Rip Curl. 2011. Consulté le 18.9.2025. Tubes à 2min05 et 4min05 (ce dernier par Tom Curren).
• 9En mathématique et mécanique des fluides, dans la théorie des équations hyperboliques, on parle de « choc ».
• 10Ce sont les deux vagues derrière les premiers surfeuses et surfeurs, visibles sur la Figure 1, et aussi sur la Figure 3. Le choc est alors qualifié de « choc dispersif ».
• 11Tissier et al. (2011) Nearshore Dynamics of Tsunami-like Undular Bores using a Fully Nonlinear Boussinesq Model. Journal of Coastal Research, pp. 603-607.
• 12Voir également les autres articles, dans la presse spécialisée, de P. Bonneton, D. Lannes, M. Ricchiuto et leurs collègues sur le sujet.