Dynamique des flots de Reeb en dimension 3
Vincent Colin, professeur à l’Université de Nantes (Laboratoire de Mathématiques Jean Leray), Pierre Dehornoy, maître de conférences à l’Université Grenoble-Alpes (Institut Fourier) et Ana Rechtman, maîtresse de conférences à l’Université de Strasbourg (Institut de recherche mathématique avancée), présentent leurs travaux en collaboration avec le professeur Umberto Hryniewicz, de l’Université d’Aix-la-Chapelle, portant sur la dynamique des flots de Reeb en dimension 3 et publiés dans Inventiones mathematicae.
1. Dynamique, chaos et surfaces
L’étude du problème des trois corps en mécanique céleste par Poincaré marqua, en 1890, la naissance de la théorie moderne des systèmes dynamiques [16]. Il découvrit alors un phénomène important : l’apparition du chaos dans une évolution pourtant régie par des lois déterministes. L’archétype de ces phénomènes est le fer-à-cheval de Smale qui décrit une orbite hyperbolique au voisinage de laquelle s’accumulent un nombre croissant exponentiellement (en fonction de la période) d’autres orbites périodiques obtenues après des successions de bifurcations. Ces propriétés rendent les trajectoires impossibles à prévoir à long terme si on a la moindre incertitude sur la position initiale. On peut quantifier cette dispersion avec la notion d’entropie topologique qui est ainsi l’outil privilégié pour mesurer les comportements chaotiques. Un autre outil fructueux – introduit par Poincaré et dont Birkhoff se saisira pleinement – est la notion de section transverse, laquelle permet de réduire certains systèmes dynamiques en dimension 3 à des systèmes en dimension 2.
Notre travail prolonge l’étude de ces notions, dans le cadre plus général des flots de Reeb tridimensionnels.
2. Les trois corps et au-delà
On considère trois corps en interaction gravitationnelle, deux massifs – le soleil et la terre – et le troisième de masse négligeable – un satellite. Pour simplifier, on suppose que la terre et le soleil ont un mouvement circulaire et que le satellite évolue dans le même plan. On parle du problème des trois corps planaire restreint. Dans un repère tournant dirigé par l’axe terre-soleil et basé au centre des masses, les deux points massifs sont immobiles et la trajectoire du satellite dans l’espace des phases position-vitesse (q,p) ∈ R2 ×R2 de dimension 4 suit une équation différentielle ordinaire de Newton d’ordre 1
(q,˙ p˙) = X(q,p)
où
ιX(dp ∧ dq) = −dH.
Ici le hamiltonien H : R4 → R représente l’énergie mécanique du système. La 2-forme dp ∧ dq est le prototype – et même le modèle local – d’une forme symplectique. Au cours du mouvement, l’énergie mécanique est préservée et on peut donc s’intéresser aux trajectoires du champ de vecteurs X sur les niveaux de H.
Lagrange au XVIIIème siècle étudia les points (et valeurs) critiques de la fonction H : il y en a cinq, ordonnés par niveaux d’énergie croissants, appelés aujourd’hui les points de Lagrange L1, L2, L3, L4 et L5. Ceux-ci interviennent actuellement dans la planification de missions spatiales, en particulier le télescope James Webb est placé au point L2 du système soleil–terre–télescope.
Les niveaux réguliers de H forment des sous-variétés de dimension 3 de l’espace des phases et sous une condition de convexité, vérifiée notamment pour de petites énergies (inférieures à H(L1)+ε), le champ de vecteurs X est un champ de Reeb [1]. On passe ici sous silence la difficulté des collisions qui peut se régler par éclatement de l’espace ambiant.
Les champs de Reeb décrivent de nombreux autres systèmes intéressants comme les flots géodésiques sur les variétés riemanniennes – dont les orbites sont les géodésiques –, le mouvement d’une particule chargée dans un champ magnétique, le mouvement d’un fluide stationnaire, incompressible et irrotationnel, etc. En dimension 3, ils sont caractérisés par le fait d’être partout transverses à un champ de plans de contact ξ = {λ = 0}, où λ est une forme différentielle de degré un pour laquelle λ ∧ dλ est une forme volume, et d’avoir un flot préservant ξ.
Très tôt Poincaré réalisa que les problèmes de dynamique tridimensionnelle sont difficiles à maîtriser. Pour tenter de les ramener à la dimension deux, il introduisit la notion de section.
3. Sections transverses à un flot
Si V est une variété de dimension 3 et X un champ de vecteurs non singulier sur V , une section transverse de X est une surface compacte à bord S ⊂ V , dont le bord est une collection d’orbites périodiques de X et telle que X est transverse à l’intérieur de S. On dit de plus que S est une section de Birkhoff (ou Poincaré-Birkhoff si S est un disque) si l’orbite de X issue de tout point de V intersecte S en temps positif et en temps négatif. Lorsqu’une section de Birkhoff existe, la dynamique du flot de X est entièrement décrite par l’application de premier retour h : int(S) → int(S) sur l’intérieur de S, qui est un difféomorphisme. Autrement dit, V \ ∂S est l’espace total d’une fibration sur le cercle de fibre int(S) et de monodromie h. Les orbites périodiques de X, en sus de ∂S, sont en bijection avec les points périodiques de h.
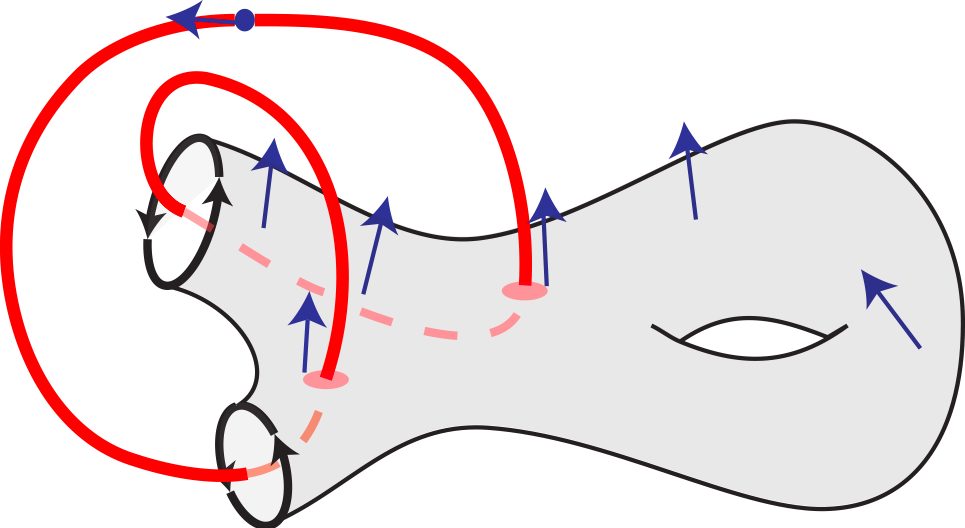
Figure 1. Une section de Birkhoff qui intersecte une orbite priodique, ici en deux points.
Dans le problème des trois corps, Poincaré trouva des sections de Birkhoff pour des valeurs très petites de l’énergie et près du soleil (le plus lourd des corps massifs). Ses résultats ont été généralisés par Birkhoff en 1927 dans le cadre des flots géodésiques des surfaces [2].
On dispose aujourd’hui de tout un arsenal de techniques et de résultats pour étudier la dynamique de h, au premier rang desquels la théorie de Nielsen-Thurston. Parmi les résultats marquants que l’on utilise dans notre étude, on cite les deux ci-dessous :
— Trois implique infini : Si h a au moins trois orbites périodiques, alors il en a une infinité.
— Généricité de l’entropie : Pour h dans un certain ouvert dense, en topologie C∞, dans les difféomorphismes de S, son entropie topologique est positive [12, 15].
4. Résultats pour des flots de Reeb génériques
Notre travail [3] et [4] montre d’une part que le phénomène décrit par Poincaré – présence de chaos représenté par une entropie topologique positive – existe génériquement parmi les champs de Reeb ; mais aussi que la situation idéale de Poincaré d’existence d’une section de Birkhoff – paradis des dynamiciens selon Ghys – est également assurée génériquement.
Théorème 4.1. [4] Sur une variété close (compacte sans bord) de dimension 3, l’ensemble des champs de Reeb qui admettent une section de Birkhoff contient un Gδ-dense en topologie C∞.
L’ensemble de ceux qui ont une entropie topologique strictement positive contient un ouvert dense en topologie C∞.
Un champ de vecteurs X est non dégénéré si pour toute orbite périodique γ de X et tout point p ∈ γ, l’application de premier retour du flot sur un petit disque transverse à X a une différentielle en p ne contenant pas 1 dans son spectre. C’est le pendant pour les champs de vecteurs de la condition de Morse pour les fonctions. Elle est C∞-générique.
Théorème 4.2. [3] Sur une variété close de dimension 3, tout champ de Reeb non dégénéré a soit 2, soit une infinité d’orbites périodiques, 2 n’étant possible que si la variété est un espace lenticulaire ou la sphère.
Ces deux résultats ont des prédécesseurs, que l’on ne décrit pas tous ici (cf. [3, 4] pour une liste plus complète). L’alternative 2 ou infini a été obtenue par Hofer, Wysocki et Zehnder dans le cas de la sphère S3, où elle donne au passage une nouvelle preuve d’un théorème fameux de Franks [8] dans le cas non dégénéré : pour toute métrique riemannienne sur la sphère de dimension 2, il y a soit 2, soit une infinité de géodésiques fermées. Le résultat de Hofer-Wysocki-Zehnder a ensuite été généralisé par Cristofaro-Gardiner, Huchings et Pomerleano [5] sur des variétés de dimension 3 quelconques mais avec une restriction sur la classe d’homotopie du champ de Reeb. L’existence de sections était, elle, plus disparate et particulière, mêlant des travaux symplectiques et des constructions plus topologiques, notamment dues à Birkhoff, Schwartzman, Fried, Sullivan entre autres. De façon un peu plus fine dans un cas particulier, Contreras, Knieper, Mazzuchelli et Shulz [7] obtiennent récemment que le flot géodésique sur une surface a, génériquement sur la métrique, une section de Birkhoff (notre condition de généricité pourrait faire sortir le flot de Reeb initial des flots géodésiques).
La clé dans la preuve de nos théorèmes est l’introduction de la notion de livre brisé portant un champ de vecteurs non singulier X et qui généralise la notion de section de Birkhoff. Au lieu que le complémentaire d’un nombre fini d’orbites périodiques K dans V soit fibré sur le cercle à fibres relativement compactes, on assouplit la condition pour demander la présence sur V \K d’un feuilletage F dont les feuilles sont relativement compactes et transverses à X. Les feuilles arrivent sur K de deux façons différentes, soit comme dans le cas des sections de Birkhoff de manière transversalement radiale, soit de manière transversalement hyperbolique (Figure 2).
Nous montrons alors :
Théorème 4.3. [3] Si V est close de dimension 3, tout champ de Reeb non dégénéré sur V est porté par un livre brisé (K,F).
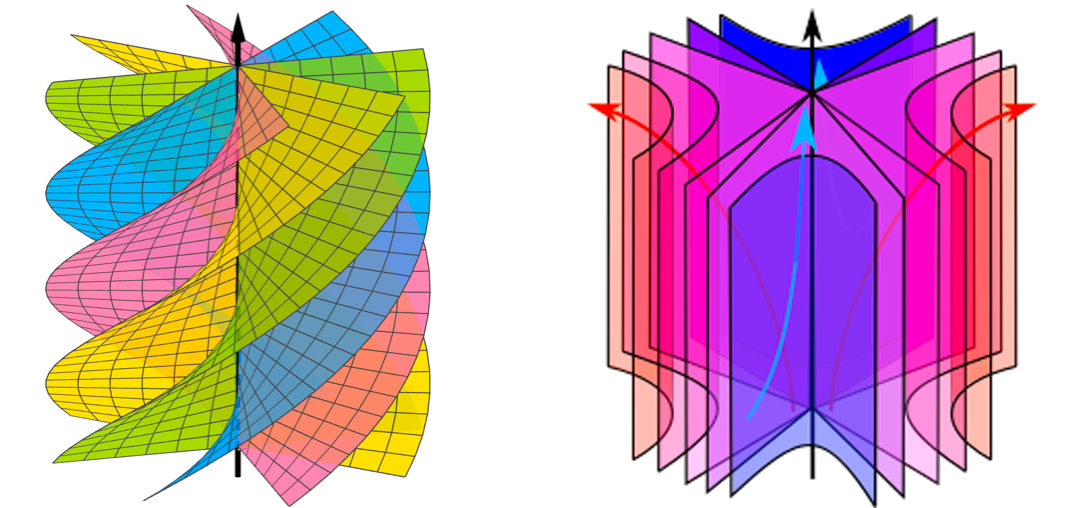
Figure 2. Les deux comportements possibles du feuilletage F près d’une composante de K : le cas radial à gauche et le cas transversalement hyperbolique droite.
Par une application directe du théorème de Stokes, un champ de Reeb ne peut jamais être transverse à une surface close. D’autre part, un champ de Reeb sans orbite périodique est non dégénéré. Le théorème 4.3 implique donc K ≠ ∅ et le fait que tout champ de Reeb possède une orbite périodique : la conjecture de Weinstein prouvée par Taubes en 2006 [18]. Ce n’est pas une surprise au vu des techniques utilisées qui incluent celles de Taubes. On note au passage que l’existence d’orbites périodiques est une illustration de la spécificité des champs de Reeb : on sait depuis les travaux de Kuperberg [14] que la sphère de dimension 3 possède un champ de vecteurs lisse sans orbites périodiques.
5. Ingrédients
La preuve du théorème 4.3 s’appuie sur des outils sophistiqués : les courbes pseudo-holomorphes dans la symplectisation d’une variété de contact. Elles interviennent dans la définition de différentielles dans des théories homologiques de type Floer (Morse) sur l’espace des lacets de V, pour une fonctionnelle d’action dont les points critiques sont les orbites périodiques du flot de Reeb. L’une d’entre elles, l’homologie de contact plongée [10], est connue pour fournir un invariant topologique de V, isomorphe à l’homologie de Seiberg-Witten [13] et de Heegaard Floer [6]. De ces isomorphismes, on retient le fait que par tout point dans la symplectisation R×V de V passe une courbe pseudo-holomorphe. La projection dans V d’une telle courbe donne une section (singulière). En considérant assez de ces sections de sorte qu’elles coupent toutes les orbites du flot de X, et en résolvant leurs intersections par un procédé de Fried [9] de même que leurs singularités, on aboutit au livre brisé.
Pour la preuve du théorème 4.1, on commence avec un champ de Reeb nondégénéré et donc porté par un livre brisé. Le passage du livre brisé (K,F) à une section de Birkhoff se fait en ajoutant à la reliure K de nouvelles orbites périodiques obtenues grâce à une loi de Weyl exploitée par Irie [11] : les orbites périodiques d’un champ de Reeb générique s’équirépartissent dans V pour une mesure de volume λ∧ dλ canoniquement associée au problème. Ce résultat permet d’obtenir une collection d’orbites périodiques K0 ⊃ K avec laquelle le flot de X a un enlacement > 0. Avec K, le livre brisé donnait seulement un enlacement du flot ≥ 0. On peut alors utiliser un critère homologique de Fried-Sullivan-Schwartzman [17] basé sur la théorie des cycles asymptotiques pour conclure à l’existence d’une section de Birkhoff.
La partie du théorème 4.1 qui porte sur l’entropie topologique utilise les travaux de Le Calvez et Sambarino [15] adaptés au cas de surfaces à bord, telles que les sections de Birkhoff.
6. Retour aux sources
Notre construction de sections de Birkhoff repose sur une machinerie imposante, développée dans les 30 dernières années et où s’entremêlent analyse, topologie et systèmes dynamiques. Elle éclaire a posteriori la fécondité de la question de Poincaré – mais qui pouvait en douter ?
Malheureusement, notre résultat d’existence ne s’applique pas directement au problème des trois corps. En perturbant le champ de Reeb dans un espace de paramètres de dimension infinie – difféomorphe à celui des fonctions positives sur V – on risque de sortir de la situation physique où les paramètres modifiables sont typiquement les deux masses et l’énergie mécanique : 3 degrés de liberté.
Peut-on sous cette contrainte trouver un livre brisé porteur ou mieux encore une section de Birkhoff ? En tout cas, la propriété de non dégénérescence du champ de Reeb qu’on utilise ne porte en fait que sur des orbites de longueur a priori bornée, ce qui en fait une condition ouverte. Un autre angle d’attaque est de produire de telles structures dans des cas concrets, ou de chercher à exploiter le caractère analytique du hamiltonien. L’alternative 2 ou infini reste en particulier ouverte pour les champs de Reeb quelconques, y compris dans le problème des trois corps.
Références
[1] P. Albers, U. Frauenfelder, O. van Koert, & G. Paternain, Contact geometry of the restricted three-body problem, Comm. Pure Appl. Math. 65 (2012), no. 2, 229–263.
[2] G. D. Birkhoff, On the periodic motions of dynamical systems, Acta Math. 50 (1927), no. 1, 359–379.
[3] V. Colin, P. Dehornoy & A. Rechtman, On the existence of supporting broken book decompositions for contact forms in dimension 3, Invent. Math. (2022).
[4] V. Colin, P. Dehornoy, U. Hryniewicz & A. Rechtman, Generic properties of 3-dimensional Reeb flows : Birkhoff sections and entropy, arXiv:2202.01506
[5] D. Cristofaro-Gardiner, M. Hutchings and D. Pomerleano, Torsion contact forms in three dimensions have two or infinitely many Reeb orbits, Geom. Topol. 23 (2019), no. 7, 3601– 3645.
[6] V. Colin, P. Ghiggini & K. Honda, The equivalence of Heegaard Floer homology and embedded contact homology via open book decompositions I, II, & III, arXiv:1208.1074 arXiv:1208. 1077arXiv:1208.1526.
[7] G. Contreras, G. Knieper, M. Mazzucchelli & B. Schulz, Surfaces of section for geodesic flows of closed surfaces, arXiv:2204.11977.
[8] J. Franks, Geodesics on S2 and periodic points of annulus homeomorphisms, Invent. Math. 108 (1992), no. 2, 403–418.
[9] D. Fried, Transitive Anosov flows and pseudo-Anosov maps, Topology 22 (1983), no. 3, 299– 303.
[10] M. Hutchings, Lectures notes on embedded contact homology. Contact and symplectic topology, 389–484, Bolyai Soc. Math. Stud. 26, Springer, 2014.
[11] K. Irie, Equidistributed periodic orbits of C∞-generic three-dimensional Reeb flows, J. Symplectic Geom. 19 (2021), no. 3, 531–566.
[12] A. Katok, Lyapunov exponents, entropy and periodic orbits for diffeomorphisms, Inst. Hautes Etudes Sci. Publ. Math. 51 (1980), 137–173.´
[13] C. Kutluhan, Y.-J. Lee & C. H. Taubes, HF=HM I : Heegaard Floer homology and Seiberg– Witten Floer homology, Geom. Topol. 24 (2020), 2829–2854.
[14] K. Kuperberg, A smooth counterexample to the Seifert conjecture, Ann. of Math. (2) 140 (1994), 723–732.
[15] P. Le Calvez & M. Sambarino, Homoclinic orbits for area preserving diffeomorphisms of surfaces, Ergodic Theory Dynam. Systems 42 (2022), no. 3, 1122–1165.
[16] H. Poincaré, Sur le problème des trois corps et les équations de la dynamique, Acta Mathematica 13 (1890), 1–270.
[17] S. Schwartzman, Asymptotic cycles, Ann. of Math. (2) 66 (1957), 270–284.
[18] C. H. Taubes, The Seiberg-Witten equations and the Weinstein conjecture. Geom. Topol. 11 (2007), 2117–2202.
Contacts
V. Colin, Nantes Université, CNRS, Laboratoire de Mathématiques Jean Leray, LMJL, F-44000 Nantes, France
- E-mail address: vincent.colin@univ-nantes.fr
- URL: https://www.math.sciences.univ-nantes.fr/~vcolin/
P. Dehornoy, Univ. Grenoble Alpes, CNRS, Institut Fourier, F-38000 Grenoble, France
- E-mail address: pierre.dehornoy@univ-grenoble-alpes.fr
- URL: http://www-fourier.ujf-grenoble.fr/~dehornop/
U. Hryniewicz, Chair of Geometry and Analysis, RWTH Aachen, Jakobstrasse 2,
52064 Aachen, Germany
- E-mail address: hryniewicz@mathga.rwth-aachen.de
- URL: https://www.mathga.rwth-aachen.de/~hryniewicz/home/
A. Rechtman, Institut de Recherche Mathématique Avancée, Université de Strasbourg, 7 rue Renée Descartes, 67084 Strasbourg, France
- E-mail address: rechtman@math.unistra.fr
- URL: https://irma.math.unistra.fr/~rechtman/
