Effet tunnel magnétique
V. Bonnaillie-Noël, directrice de recherche au CNRS, F. Hérau, professeur à l'université de Nantes et N. Raymond, professeur à l'université d'Angers, décrivent une formule récemment démontrée dans « Pure magnetic tunneling effect in two dimensions », paru à Inventiones Mathematicae, qui trouve ses origines et ses motivations dans la physique quantique.
1. Les motivations
1.1. Les origines physiques d'un problème mathématique
La formule dont cet article résume l'histoire et qui a été démontrée dans notre travail [6] trouve ses origines et ses motivations dans la physique quantique. C'est un très ancien problème de savoir décrire précisément les comportements des atomes et des molécules (au moins aussi vieux que Démocrite !). Notre résultat mathématique s'inscrit dans cette longue histoire, particulièrement dans ses développements spectaculaires du début du 20ème siècle, avec la naissance de la physique quantique. L'équation de Schrödinger est l'une des équations qui gouvernent le monde nanoscopique :
\[\left((-ih\nabla-\mathbf{A})^2+V\right)\Psi=ih\partial_t\Psi\,.\]
Ici $\mathbf{A}$ et $V$ désignent le potentiel vecteur et le potentiel électrique, respectivement : ce sont les sources du champ électro-magnétique $(\mathbf{E},\mathbf{B})=(\nabla V,\nabla\times\mathbf{A})$. La recherche de solutions particulières conduit à chercher des solutions sous la forme
\[\Psi(x,t)=\varphi(x)e^{-i\lambda t/h}\,,\]
et cela fait apparaître un problème aux valeurs propres1
:
\begin{equation}\label{eq.eve}
\left((-ih\nabla-\mathbf{A})^2+V\right)\varphi=\lambda\varphi\,. \quad (1.1)
\end{equation}
La recherche de solutions $(\lambda,\varphi)$ à cette équation est encore un domaine actif de la recherche mathématique, notamment dans la limite $h\to 0$ (dite "régime semiclassique"2
). Nombre de résultats très avancés furent obtenus dans les années 80, avec les travaux fondateurs de Helffer et Sjöstrand (voir l'impressionnante série de travaux [13, 15, 14, 16, 17, 19, 18]), notamment dans le cas sans champ magnétique $\mathbf{A}=0$. Un phénomène physique qui les a particulièrement intéressés et auquel ils ont fourni une explication mathématique très avancée est celui de l'effet tunnel. Cet effet se produit quand le potentiel électrique $V$ possède des symétries3
. Prenons par exemple un potentiel électrique de la forme donnée à la figure 1.
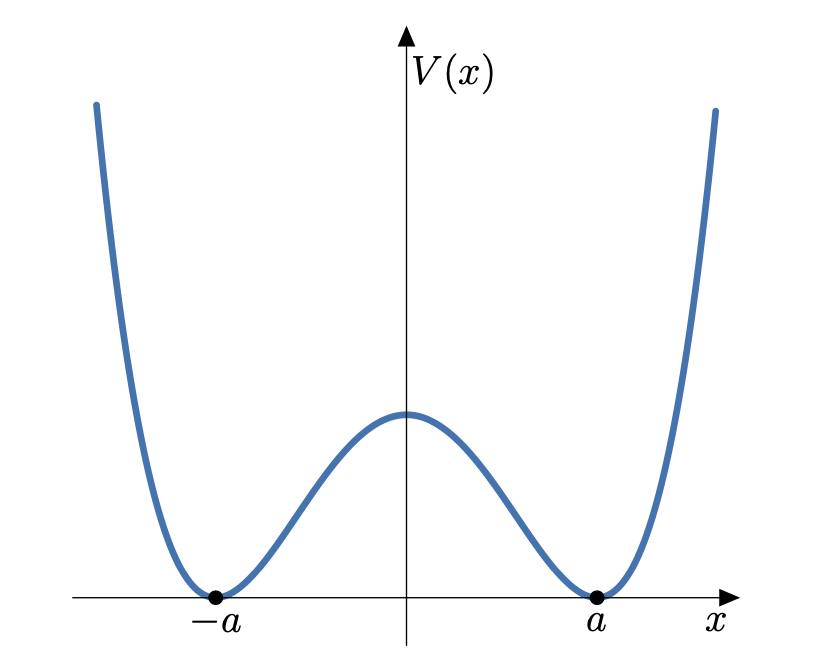
FIGURE 1. Potentiel électrique à double puits
Dans ce cas, la différence entre les deux plus petites valeurs propres $\lambda_1(h)$ et $\lambda_2(h)$ est exponentiellement petite et vérifie4
\[\lambda_2(h)-\lambda_1(h)\underset{h\to0}{=}A\sqrt{h}e^{-S/h}+o(\sqrt{h}e^{-S/h})\,,\quad S=\int_{-a}^a \sqrt{V(x)}\mathrm{d}x\,,\]
et où $A>0$ est une constante qu'on peut expliciter en fonction de $V$. Malgré la symétrie de $V$, la plus petite valeur propre n'est pas double (même si elle l'est presque, à un facteur exponentiellement petit près : c'est un peu cela l'effet tunnel).
En fait, on peut montrer que $\lambda_1(h)<\lambda_2(h)$ et que les deux premières fonctions propres normalisées associées à $\lambda_1(h)$ et $\lambda_2(h)$, notées $\psi_1$ et $\psi_2$, sont respectivement paire et impaire. Posant $\psi_0=\psi_1+\psi_2$ et faisant évoluer cette fonction par l'équation de Schrödinger, on voit que la solution s'écrit
\[\psi(x,t)=e^{it\lambda_1(h)/h}\psi_1(x)+e^{it\lambda_2(h)/h}\psi_2(x)\,.\]
Un petit calcul élémentaire montre alors que
\[|\psi(x,t)|^2=|\psi(-x,t+T)|^2\,,\quad T=\frac{\pi h}{\lambda_2(h)-\lambda_1(h)}\,.\]
Ainsi, si $\psi_0$ est localisée près du minimum de droite, au bout d'un temps $T$ exponentiellement grand, elle se localise au minimum de gauche ! Ce déplacement de masse à travers le maximum local en $0$ est l'effet tunnel. Une connaissance précise de $\lambda_2(h)-\lambda_1(h)$ permet de caractériser la période de ce phénomène.
Lorsque le champ magnétique est non nul mais que $V=0$, cet effet est encore largement méconnu mathématiquement : le seul résultat connu est celui auquel cet article est consacré.
En fait, d'autres motivations physiques amènent à étudier (1.1), dont la supraconductivité. Ce phénomène se produit pour certains matériaux à des températures très basses : il se mettent à jouir d'une conductivité infinie... et à détester les champs magnétiques. Cela donne lieu à des expériences de lévitation qu'on peut réaliser assez facilement en public5 . Ce qui est remarquable, c'est que les seules explications de ce phénomène observable à l'échelle humaine sont d'ordre quantique. Au cœur de ces phénomènes, un modèle proposé par Pierre-Gilles de Gennes fait intervenir l'équation (1.1) : elle permet de comprendre la supraconductivité de surface (c'est là que la supraconductivité perdure le plus) dont certains aspects mathématiques sont décrits dans l'ouvrage [10].
Nos motivations sont donc à la confluence de plusieurs considérations physiques (modèles de Schrödinger, modèles phénoménologiques de la supraconductivité), mais aussi de plusieurs domaines des mathématiques : les équations aux dérivées partielles, l'analyse hilbertienne et la théorie spectrale, l'analyse semiclassique (une généralisation de l'analyse de Fourier, avec un petit paramètre lié à la constante de Planck), l'analyse numérique et même d'autres domaines allant jusqu'à la géométrie symplectique.
1.2. Une brève histoire magnétique
Maintenant que nous savons pourquoi nous faisons ce que nous faisons (du reste, le croyons-nous !), il va bien falloir dire quelques mots des mathématiques... Le lectorat (très) curieux peut consulter le livre [23] pour plus d'informations.
1.2.1. Le Laplacien magnétique
Considérons un ouvert $\Omega\subset\mathbf{R}^2$ régulier, connexe et simplement connexe (un gentil patatoïde donc). Le Laplacien de Neumann avec champ magnétique constant est l'opérateur différentiel agissant comme
\[\mathscr{L}_{h}=(-i h\nabla-\mathbf{A})^2\,,\quad\mbox{ avec }\quad B:=\partial_{x_1}A_2-\partial_{x_2}A_1=1\,,\quad h>0\,,\]
sur les fonctions de l'espace suivant
\begin{equation*}
\mathrm{Dom}(\mathscr{L}_h)=\big\{\psi\in H^1(\Omega) : (-ih\nabla-\mathbf{A})^2\psi\in L^2(\Omega)\,, \end{equation*}
\begin{equation*} \mathbf{n}\cdot(-ih\nabla-\mathbf{A})\psi=0 \mbox{ sur } \partial\Omega\big\}\,,
\end{equation*}
$\mathbf{n}$ étant la normale sortante.
Dans le cas où le potentiel vecteur $\mathbf{A}$ est linéaire, le champ magnétique $B$ est constant. Par exemple, avec $\mathbf{A}(x)=(-x_2,0)$, on a $B=1$ et on peut même déterminer le spectre quand $\Omega=\mathbb{R}^2$ (formé de valeurs propres de multiplicité infinie) :
\[\mathrm{sp}(\mathscr{L}_h)=\{(2n-1)h\,,\quad n\geq 1\}\,.\]
Lorsque $\Omega$ est borné, le spectre de cet opérateur est discret (il est constitué de valeurs propres isolées de multiplicité finie) ; la suite croissante de ses valeurs propres est notée $(\lambda_j(h))_{j\geq 1}$. Nous nous intéressons au comportement de ces dernières dans la limite dite semiclassique $h\to 0$, ainsi qu'aux fonctions propres associées, aussi bien théoriquement que numériquement.
1.2.2. Le cas du champ magnétique constant
Lorsque $\Omega$ est le demi-plan
\[\mathbf{R}^2_+=\{(s,t)\in\mathbf{R}^2 : t>0\}\,,\]
l'opérateur agit comme
\[\mathscr{L}_h=-h^2\partial^2_t+(-ih\partial_s-t)^2\,,\]
muni de la condition de Neumann en $t=0$. On peut utiliser la transformée de Fourier en $s$ et on fait apparaître une famille d'opérateurs en une dimension, dépendant du paramètre de Fourier $\xi$. Pour chaque $\xi\in\mathbf{R}$, on voit surgir l'opérateur6
, agissant sur $L^2(\mathbf{R}_+)$ comme
\[\mathscr{M}_\xi=-\partial_t^2+(\xi-t)^2\,,\mbox{ avec condition de Neumann en $t=0$}\,.\]
Le bas du spectre de cet opérateur est une valeur propre simple notée $\mu(\xi)$. Sa fonction propre associée, positive et normalisée, est notée $u_\xi$. Les fonctions $\xi\mapsto\mu(\xi)$ et $\xi\mapsto u_{\xi}$ sont analytiques en $\xi$. Par le travail de Dauge et Helffer [7], on sait qu'il existe $\xi_0>0$ tel que $\mu$ est décroissante sur $(-\infty,\xi_0)$ et croissante sur $(\xi_{0},+\infty)$. On pose :
\[\mathbf{\Theta_0}:=\mu(\xi_0)\,, \qquad \mathbf{C_1}:=\frac{|u_{\xi_0}(0)|^2}{6}\,,\]
et on peut montrer les relations structurelles suivantes:
\[\mathbf{\Theta_0}=\xi_0^2\in]0,1[\,,\quad \mathbf{C_1}=\frac{\mu''(\xi_0)}{12\xi_0}>0\,.\]
1.2.3. Des valeurs propres aux approximations optimales des fonctions propres
Lorsqu'on quitte l'univers bien plat du demi-plan et qu'on s'aventure dans la géométrie plus courbe d'un ouvert $\Omega$ borné (comme un disque), il est assez naturel de se demander quelle pourrait être l'influence de la courbure sur l'asymptotique des valeurs propres. C'est d'autant plus tentant que certains modèles et expériences de la physique de la supraconductivité conduisent à penser que la courbure joue un rôle fondamental dans la supraconductivité de surface (les "paires de Cooper" se localisent près du bord, mais pas uniformément : elles sont concentrées près des points de courbure maximale). Voici un résultat qui manifeste l'importance de la courbure dans le cas d'un ouvert $\Omega$. Il a été obtenu par Helffer et Morame qui menaient déjà une collaboration sur le laplacien magnétique depuis plusieurs années, pour des raisons a priori indépendantes de la supraconductivité (et qui relèvent de problèmes d'hypoellipticité7 ). Voici donc leur remarquable résultat8 .
Théorème 1.1 (Helffer - Morame 2001, [12]). On a le développement limité suivant :
\begin{equation*}\label{eq.hm}
\lambda_1(h)\underset{h\to 0}{=}\mathbf{\Theta_0} h-\mathbf{ C_1}\kappa_{\max}h^{\frac 32}+o(h^{\frac 32})\,,
\end{equation*}
où $\kappa_{\max}$ est le maximum de la courbure de $\partial\Omega$.
On ne s'étonnera pas de retrouver le fameux $\mathbf{\Theta_0}$. En effet, au voisinage du bord, $\Omega$ ressemble fort à $\mathbf{R}^2_+$ et le laplacien magnétique se réduit à l'opérateur de de Gennes. Les approximations diverses d'Helffer et Morame au voisinage du bord sont justifiées car les fonctions propres associées à $\lambda_1(h)$ sont exponentiellement concentrées près du bord sur un voisinage d'épaisseur $\sqrt{h}$. Cette propriété se démontre à l'aide des estimations d'Agmon9 (revisitées dans un contexte semiclassique dans les années 80 par Helffer et Sjöstrand).
La lectrice avisée et exigeante fera remarquer que nous avons promis de parler des autres valeurs propres $\lambda_2(h)$, $\lambda_3(h)$... Il faut attendre quelques années avant d'en savoir plus sur le spectre avec le développement asymptotique à tout ordre de chaque valeur propre obtenu par Fournais et Helffer.
Théorème 1.2 (Fournais - Helffer 2006, [9]). Supposons que $\partial\Omega$ possède un unique point de courbure maximale, lequel est non-dégénéré. Alors, pour tout $n\geq 1$,
\begin{equation*}
\lambda_{ n}(h)=\mathbf{\Theta_0} h-\mathbf{ C_1}\kappa_{\max}h^{\frac 32}+(2 n-1)\mathbf{C_1\Theta^{\frac 14}_0}\sqrt{\frac{3k_2}{2}}h^{\frac 74}+o(h^{\frac 74})\,, \end{equation*}
\begin{equation*} k_2=-\kappa''(s_{\max})\,,
\end{equation*}
où $\kappa$ est la courbure vue comme fonction de l'abscisse curviligne et $s_{\max}$ l'abscisse du maximum de la courbure.
Le lecteur attentif nous interpellera à nouveau : mais où sont donc les fonctions propres ? À quoi ressemblent-elles ? La curiosité est un vilain défaut... à entretenir. Nous allons revenir bientôt sur cette question essentielle. Au début des années 2000, la thèse [2] fut motivée notamment par l'analyse numérique des valeurs propres et des fonctions propres. L'autrice s'est intéressée à des ouverts non réguliers (notamment les polygones) et nous commençâmes à visualiser les fonctions propres. Les simulations devinrent de plus en plus précises, notamment à l'aide de la bibliothèque d'éléments finis Mélina et des collaborations avec Monique Dauge10 , Daniel Martin et Grégory Vial [3].
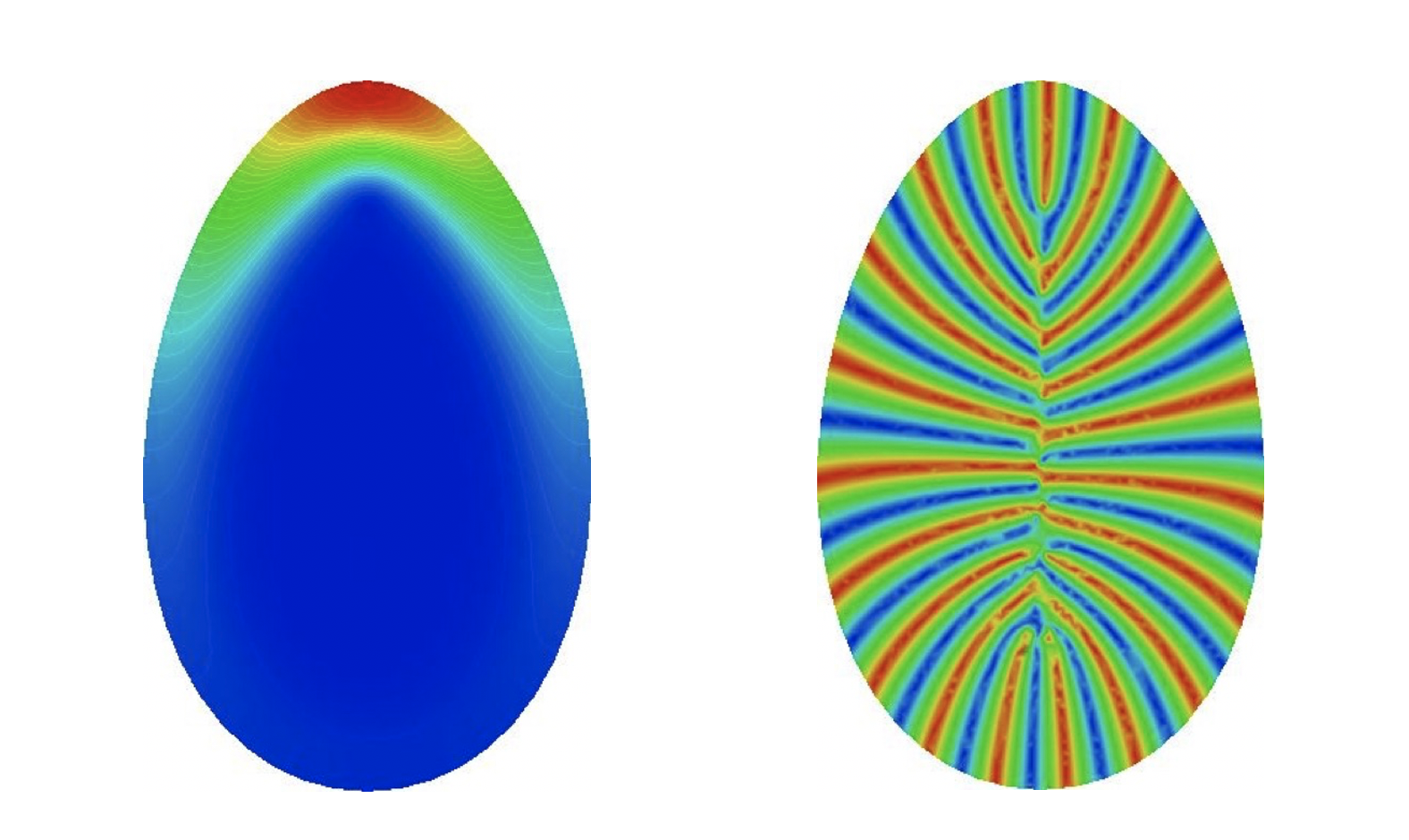
FIGURE 2. Simulation des module et argument d'une fonction propre associée à $\lambda_1(h)$, sur... un œuf de Pâques !
Sur la figure 2, nous voyons nettement le caractère attractif de l'unique point de courbure maximale. Dans le cas où l'ouvert est un carré, ce sont les coins qui attirent les fonctions propres11 . Il est même possible de tracer les valeurs propres (voir la figure 3). Il est frappant que les méthodes numériques mises en place permettent de décrire de tels effets d'oscillation des valeurs propres et de capturer un rapprochement exponentiel des quatre premières valeurs propres.
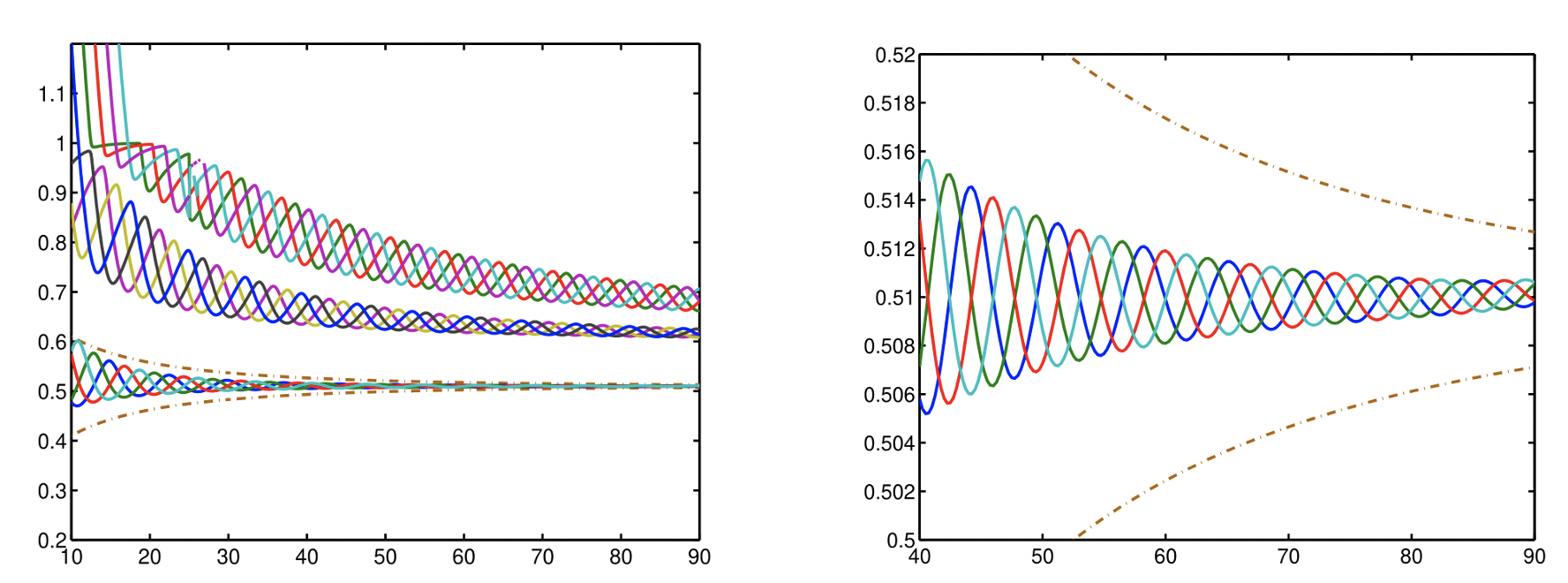
FIGURE 3. Les premières valeurs propres du carré $[-1,1]^2$ (divisées par $h$) en fonction de $1/h$ (les quatre premières à droite)
Revenons au problème de décrire les fonctions propres. Une question longtemps ouverte (probablement depuis les années 90) concernant le Laplacien magnétique était de savoir si ses fonctions propres pouvaient être approchées par une méthode BKW (du nom de Brillouin, Kramers et Wentzel). Autrement dit, peut-on approcher les fonctions propres magnétiques par des fonctions de la forme $a(s,t,h)e^{-\Phi(s,t)/h^\alpha}$12 ? Une réponse positive et plutôt générale fut donnée dans notre travail [5]. Sous les hypothèses de Fournais et Helffer, nous avons obtenu en particulier le théorème suivant.
Théorème 1.3 (Bonnaillie-Noël - Hérau - Raymond 2016, [5]). Pour tout $n\geq 1$, la fonction suivante est une approximation locale, près de $s_{\max}$, dans $L^2$ de la $n$-ième fonction propre de $\mathscr{L}_h$ :
\[ \Psi^{\mathrm{BKW}}_{n,h}(s,t)=e^{-\Phi(s)/h^{\frac 14}}u_{\xi_0}(h^{-\frac{1}{2}}t)f_{n,0}(s)\,.\]
où \[\Phi(s)=\sqrt{\frac{2\mathbf{C_1}}{\mu''_1(\xi_0)}}\int_{[s_{\max},s]}\sqrt{\kappa_{\max}-\kappa(\sigma)}\mathrm{d}\sigma\,,\]
et où $f_{n,0}$ résout l'équation de transport effective
\begin{equation*}
\frac{\mu''_1(\xi_0)}{2}(\Phi'\partial_\sigma+\partial_{\sigma}\Phi')f_{n,0}+F(\sigma)f_{n,0}=(2n-1)\mathbf{C_1\Theta_0^{\frac 14}}\sqrt{\frac{3k_2}{2}}f_{n,0}\,,
\end{equation*}
et où $F$ est une fonction régulière telle que $F(s_{\max})=0$ et $\mathrm{Re} F=0$.
Il est remarquable de voir la géométrie (décrivant l'espace) se marier à la fonction de de Gennes (où intervient la fréquence) dans la phase $\Phi$ de l'approximation BKW. Et d'où vient la puissance $\frac14$ ? Fort heureusement, nous n'avons pas besoin d'avoir toutes les réponses à nos interrogations pour explorer numériquement une autre question naturelle : l'effet des symétries. Imaginons qu'il y ait deux points de courbure maximale et, pour simplifier, que $\Omega$ soit symétrique par rapport à un axe (celui des ordonnées). Nous sommes bien vite amenés à penser au cas d'une ellipse et à nous tourner avec curiosité vers les simulations numériques.
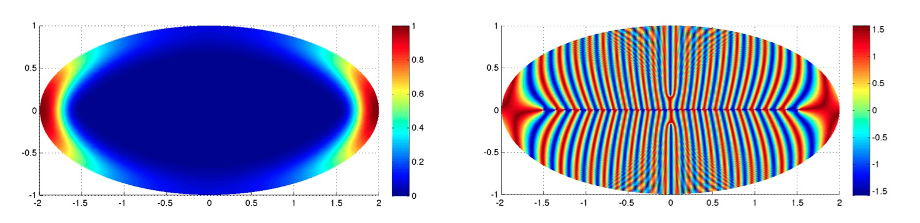
FIGURE 4. Module et argument de la première fonction propre
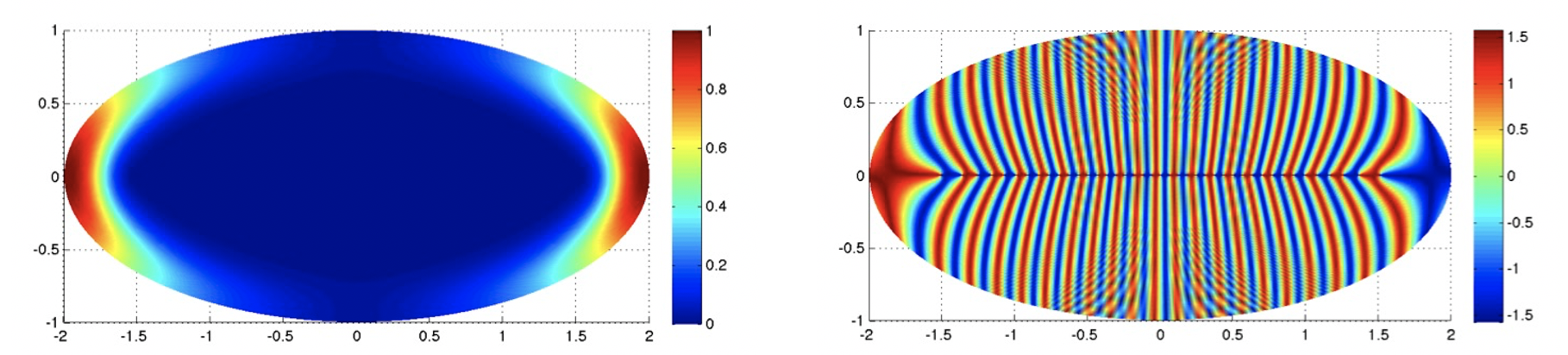
FIGURE 5. Module et argument de la deuxième fonction propre
Les fonctions propres associées à $\lambda_1(h)$ et $\lambda_2(h)$ se ressemblent beaucoup par l'intensité, mais diffèrent par la phase. Les valeurs propres se ressemblent-elles autant ? Oui, comme on peut le voir sur la figure 6, où apparaît la différence $\lambda_2(h)-\lambda_1(h)$.
FIGURE 6. $\lambda_2(h)-\lambda_1(h)$ en fonction de $1/h$
L'écart des deux premières valeurs propres semble tendre exponentiellement vers $0$ en devenant nul par intermittence.
2. Vingt ans après Helffer-Morame : la formule d'effet tunnel
Il faut attendre cinq années supplémentaires après [5] pour démontrer une formule qui explique la figure 6. La voici.
Théorème 2.1 (Bonnaillie-Noël - Hérau - Raymond 2021, [6], cas de l'ellipse). Il existe un nombre $\alpha_0\in\mathbf{R}$ tel que
\begin{equation*}
\lambda_{2}(h)-\lambda_{1}(h)\!\underset{\hbar\to 0}{\sim}\!
h^{\frac{13}{8}} a \mathsf{A}
\left|\cos\left(L\left(\frac{\gamma_{0}}{h}-\frac{\xi_{0}}{h^{\frac12}}-
\alpha_0\right)\right) \right|
\mathrm{e}^{-{\mathsf{S}}/{h^{\frac{1}{4}}}}\,,
\end{equation*}
où
\begin{equation*}
\begin{split}
\mathsf{S}&=
\sqrt{\frac{2C_{1}}{\mu_1''(\xi_{0})}}\int_{-\frac L2}^{\frac L2}\sqrt{\kappa_{\max}-\kappa(s)}\,{\rm d} s\,,\\
\mathsf{A} &=\exp\left(-\int_{[\frac L2, L]}\frac{\partial_{s}\sqrt{\kappa_{\max}-\kappa(s)}-\sqrt{\frac{k_2}{2}}}{\sqrt{\kappa_{\max}-\kappa(s)}}\,{\rm d} s\right)\,,\\
a&=\frac{2^{\frac{5}{2}} C_1^{\frac{3}{4}}}{\sqrt{\pi}} \left(k_2\mu_1''(\xi_0)\right)^{\frac{1}{4}}
\left(\kappa_{\max}-\kappa_{\min}\right)^{\frac{1}{2}}\,,\\
\gamma_0&=\frac{|\Omega|}{|\Gamma|}=\frac{|\Omega|}{2L}\,.
\end{split}
\end{equation*}
Ici, les points $s=-\frac{L}{2}$ et $s=\frac{L}{2}$ correspondent aux maxima de la courbure à droite et à gauche, respectivement. $L$ est le demi-périmètre de l'ellipse.
Le théorème précédent est un cas particulier de celui que nous avons établi dans notre article [6]. Le cosinus qui apparaît dans le préfacteur de l'exponentielle est dû à la présence de la symétrie par rapport à l'axe des abscisses. Dans cette situation, il coûte aussi cher de voyager sur le bord pour aller d'un maximum de courbure à l'autre en passant par le haut qu'en passant par le bas. Le prix à payer est directement lié à $\mathsf{S}$, distance d'Agmon effective, interne au bord, entre les points de courbure maximale. Il est frappant d'avoir une formule aussi explicite qui traduit la façon dont ces points communiquent par "effet tunnel". Comme dans le cas électrique, cet effet est exponentiellement petit et est déterminé par le comportement exponentiellement décroissant des fonctions propres loin des points de courbure maximale. Décrire rigoureusement cette décroissance le long du bord (dans la zone en bleu, voir les figures 4 et 5) a été le cœur de notre travail. La superposition des simulations numériques pour l'ellipse et du tracé de notre formule fournit la figure 7.
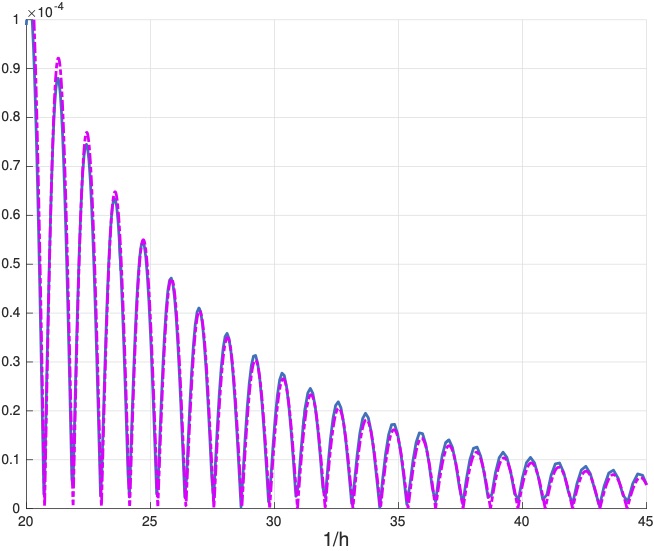
FIGURE 7. $\lambda_2(h)-\lambda_1(h)$ en fonction de $1/h$ : simulation numérique pour l'ellipse (en bleu) versus la formule du théorème 2.1 (en rose)
3. Ce qui n'apparaît pas
Il n'est pas question ici d'expliquer la preuve du théorème 2.1. Il conviendrait plutôt de dire déjà ce qu'elle n'est pas. Les nécessités d'un exposé amènent parfois à penser que les histoires mathématiques se déroulent de façon linéaire : comme si le temps écoulé entre le résultat de Helffer et Morame de 2001 et notre formule de 2021 était réparti sur une belle ligne droite, et même pire, comme si notre résultat n'était que l'issue mécanique et nécessaire des œuvres du passé. Il n'en est bien sûr rien. Qui peut prévoir l'issue d'une discussion scientifique qui a lieu fortuitement au cours d'une conférence ou après la lecture d'un article aperçu par hasard ? Ce qui n'apparaît pas dans la belle histoire linéaire, ce sont les circonvolutions incessantes, les répétitions, les échecs... Qui peut croire qu'un pianiste puisse jouer admirablement en public sans jouer d'abord hasardeusement dans le secret de ses répétitions ? Ce qui n'apparaît pas ce sont les séjours longs à l'Institut Mittag-Leffler (en 2012 et en 2019) où des idées cruciales nous sont apparues dans une bibliothèque magnifique ou encore les séjours à Aarhus (à l'invitation de S. Fournais). Ce qui n'apparaît pas, c'est le temps accordé par le CNRS via les délégations pour penser paisiblement. Ce qui n'apparaît pas, c'est l'illumination qui a lieu quand on discute autour d'un café ou qu'on s'asseoit à un piano, croyant naïvement qu'on fait une pause. Ce qui n'apparaît pas, ce sont les thèmes abordés en parallèle : la physique mathématique des guides d'ondes13 , la théorie spectrale du Laplacien de Robin14 , la géométrie symplectique et sa quantification15 , la théorie de Born-Oppenheimer16 , les méthodes des éléments finis de haut degré17 ou l'étude semiclassique des équations de Fokker-Planck18 . Tous ces thèmes sont profondément mêlés. La preuve du théorème 2.1 est irriguée par toutes ces rencontres d'idées et de personnes, à travers le temps et au delà des frontières réelles ou imaginaires.
Remerciements. Nous exprimons notre gratitude à toutes celles et tous ceux qui ont pris part à cette aventure magnétique !
- 1C'est un problème de "théorie spectrale" (théorie qu'on découvre sous des formes élémentaires en deuxième année de Licence !), un domaine qui s'est développé conjointement avec l'analyse hilbertienne au début du 20ème siècle.
- 2L'analyse semiclassique est le domaine mathématique qui explique les liens entre les équations qui gouvernent la mécanique classique (celle de Newton) et les équations de la mécanique quantique (celle de Schrödinger, de Dirac... ou d'autres !).
- 3Un exposé du séminaire Bourbaki par D. Robert dans un cadre simplifié donne un bel aperçu de l'œuvre de Helffer et Sjöstrand, cf. [24].
- 4Ce cas particulier a été traité par Harrell dans [11].
- 5Voir l'exposé de Julien Bobroff : https://youtu.be/Sj5eue4jm9c?t=4306
- 6On l'appelle souvent "opérateur de de Gennes" en raison de son rôle dans les équations de la supraconductivité manipulées par Pierre-Gilles de Gennes (1932-2007). https://fr.wikipedia.org/wiki/Pierre-Gilles_de_Gennes
- 7Ce domaine a connu des développements fondamentaux sous l'impulsion de Lars Hörmander (1931-2012) et de l'école microlocale. https://en.wikipedia.org/wiki/Lars_Hormander
- 8qui fait lui-même suite à d'autres résultats, notamment dans le cas du disque, [1]
- 9Shmuel Agmon (1922-) est notamment connu pour ses travaux sur la localisation des solutions d'EDP elliptiques. https://en.wikipedia.org/wiki/Shmuel_Agmon
- 10qui participa à une généralisation profonde [4] du résultat d'Helffer et Morame à la dimension trois pour des ouverts non réguliers, se basant sur la théorie des chaînes singulières développée par ses soins dans les années 80.
- 11Voir les nombreuses simulations présentes sur la page : http://www.math.ens.fr/bonnaillie/Schrodinger/anim.html
- 12Ici, (s,t) désigne les coordonnées tubulaires au voisinage du bord de Ω, s étant l'abscisse curviligne et t la distance au bord.
- 13avec D. Krejčiřík, M. Dauge, T. Ourmières-Bonafos
- 14avec B. Helffer et A. Kachmar
- 15avec S. Vũ Ngọc
- 16développée par A. Martinez, cf. [21, 22], en partant des idées puissantes de J. Sjöstrand autour de la théorie de Fredholm et de la méthode de Grushin (décrites pédagogiquement dans [25]) et améliorée par exemple dans la thèse de P. Keraval [20] en 2019 pour l'appliquer au Laplacien magnétique
- 17sans lesquelles l'effet tunnel magnétique n'aurait pas pu être capturé numériquement !
- 18avec M. Hitrik et J. Sjöstrand
Références
[1] P. Bauman, D. Phillips, and Q. Tang. Stable nucleation for the Ginzburg-Landau system with an applied magnetic field. Arch. Rational Mech. Anal., 142(1) :1–43, 1998.
[2] V. Bonnaillie.Analyse mathématique de la supraconductivité dans un domaine à coins : méthodessemi-classiques et numériques. PhD thesis, Université Paris 11, 2003.
[3] V. Bonnaillie-Noël, M. Dauge, D. Martin, and G. Vial. Computations of the first eigenpairs for the Schrödinger operator with magnetic field. Comput. Methods Appl. Mech. Engrg., 196(37-40) :3841– 3858, 2007.
[4] V. Bonnaillie-Noël, M. Dauge, and N. Popoff. Ground state energy of the magnetic Laplacian on corner domains. Mém. Soc. Math. Fr. (N.S.), (145) :vii+138, 2016.
[5] V. Bonnaillie-Noël, F. Hérau, and N. Raymond. Magnetic WKB constructions. Arch. Ration. Mech. Anal., 221(2) :817–891, 2016.
[6] V. Bonnaillie-Noël, F. Hérau, and N. Raymond. Pure magnetic tunnelling effect in two dimensions. To appear in Inventiones Mathematicae, 2021.
[7] M. Dauge and B. Helffer. Eigenvalues variation. I. Neumann problem for Sturm-Liouville operators. J. Differential Equations, 104(2) :243–262, 1993.
[8] M. de Montaigne. Les Essais. 1580.
[9] S. Fournais and B. Helffer. Accurate eigenvalue asymptotics for the magnetic Neumann Laplacian. Ann. Inst. Fourier (Grenoble), 56(1) :1–67, 2006.
[10] S. Fournais and B. Helffer. Spectral methods in surface superconductivity, volume 77 of Progress in Nonlinear Differential Equations and their Applications. Birkhäuser Boston, Inc., Boston, MA, 2010.
[11] E. M. Harrell. Double wells. Comm. Math. Phys., 75(3) :239–261, 1980.
[12] B. Helffer and A. Morame. Magnetic bottles in connection with superconductivity. J. Funct. Anal., 185(2) :604–680, 2001.
[13] B. Helffer and J. Sjöstrand. Multiple wells in the semiclassical limit. I. Comm. Partial Differential Equations, 9(4) :337–408, 1984.
[14] B. Helffer and J. Sjöstrand. Multiple wells in the semiclassical limit. III. Interaction through nonresonant wells. Math. Nachr., 124 :263–313, 1985.
[15] B. Helffer and J. Sjöstrand. Puits multiples en limite semi-classique. II. Interaction moléculaire. Symétries. Perturbation. Ann. Inst. H. Poincaré Phys. Théor., 42(2) :127–212, 1985.
[16] B. Helffer and J. Sjöstrand. Puits multiples en mécanique semi-classique. IV. Étude du complexe de Witten. Comm. Partial Differential Equations, 10(3) :245–340, 1985.
[17] B. Helffer and J. Sjöstrand. Puits multiples en mécanique semi-classique. V. Étude des minipuits. In Current topics in partial differential equations, pages 133–186. Kinokuniya, Tokyo, 1986.
[18] B. Helffer and J. Sjöstrand. Effet tunnel pour l’équation de Schrödinger avec champ magnétique. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4), 14(4) :625–657 (1988), 1987.
[19] B. Helffer and J. Sjöstrand. Puits multiples en mécanique semi-classique. VI. Cas des puits sous- variétés. Ann. Inst. H. Poincaré Phys. Théor., 46(4) :353–372, 1987.
[20] P. Keraval. Formules de Weyl par réduction de dimension. Applications à des Laplaciens électro- magnétiques. PhD thesis, Université de Rennes 1, 2018.
[21] A. Martinez. Développements asymptotiques et effet tunnel dans l’approximation de Born-Oppenheimer. Ann. Inst. H. Poincaré Phys. Théor., 50(3) :239–257, 1989.
[22] A. Martinez. A general effective Hamiltonian method. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl., 18(3) :269–277, 2007.
[23] N. Raymond. Bound states of the magnetic Schrödinger operator, volume 27 of EMS Tracts in Mathematics. European Mathematical Society (EMS), Zürich, 2017.
[24] D. Robert. Analyse semi-classique de l’effet tunnel. Astérisque, (145-146) :5, 257–281, 1987. Séminaire Bourbaki, Vol. 1985/86.
[25] J. Sjöstrand and M. Zworski. Elementary linear algebra for advanced spectral problems. volume 57, pages 2095–2141. 2007. Festival Yves Colin de Verdière.
Contacts
- Virginie Bonnaillie-Noël, directrice de recherche au CNRS, membre du Département de mathématiques et applications de l'ENS (DMA - UMR 8553 - CNRS & École normale supérieure), directrice de la Direction d'appui aux partenariats publics, CNRS ;
- Frédéric Hérau, professeur à l'université de Nantes, membre du Laboratoire de Mathématiques Jean Leray (LMJL - UMR6629 - CNRS & Université de Nantes) ;
- Nicolas Raymond, professeur à l'université d'Angers, membre du Laboratoire Angevin de Recherche en Mathématiques (LAREMA - UMR6093 - CNRS & Université d'Angers).
