Groupes de Cremona en dimension supérieure

L'espace projectif $\mathbb{P}^n:= \mathbb{P}^n_ \mathbb{C}$ de dimension $n\geq1$ est la variété algébrique projective la plus symétrique. Dans une carte affine, une symétrie birationnelle de $\mathbb{P}^n$ s'écrit

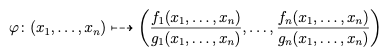
où les $f_1,\dots,f_n,g_1,\dots,g_n$ sont des polynômes non-nuls. On demande de plus qu'il existe une application $\psi$ de la même forme tel que formellement $\varphi\circ\psi=\psi\circ\varphi=id_{\mathbb{P}^n}$. Par exemple l'application

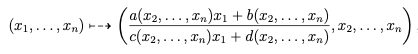
où $\left(\begin{smallmatrix}a&b\\c&b\end{smallmatrix}\right)\in PGL_2(\mathbb{C}(x_2,\dots,x_n))$ est une symétrie birationnelle de $\mathbb{P}^n$, dont l'inverse s'obtient en inversant la matrice dans $PGL_2(\mathbb{C}(x_2,\dots,x_n))$. Elle n'est pas définie en tout point de $\mathbb{P}^n$, mais elle se restreint en un isomorphisme entre des ouverts denses de Zariski.

Le groupe $Bir(\mathbb{P}^n)$ des symétries birationnelles de $\mathbb{P}^n$ s'appelle groupe de Cremona, nommé après L. Cremona, qui a fondé la théorie [Cre63, Cre65]. Le groupe de Cremona contient le groupe $Aut(\mathbb{P}^n)\simeq PGL_{n+1}(\mathbb{C})$ des automorphismes de $\mathbb{P}^n$, et en fait $Bir(\mathbb{P}^1)=Aut(\mathbb{P}^1)\simeq PGL_2(\mathbb{C})$.
Pour $n\ge 2$, l'exemple ci-dessus donne une inclusion
$$
PGL_2(\mathbb{C}(x_2,\dots,x_n))\hookrightarrow Bir(\mathbb{P}^n).
$$
En agissant birationnellement sur les variables restantes $x_2, \dots, x_n$ on obtient donc une inclusion
\[
PGL_2(\mathbb{C}(x_2,\dots,x_n))\rtimes Bir(\mathbb{P}^{n-1})\hookrightarrow Bir(\mathbb{P}^n).
\]
Ces applications sont dites de Jonquières.

Le théorème de Nœther-Castelnuovo affirme que pour $n=2$ le groupe de Cremona est engendré par $Aut(\mathbb{P}^2)$ et la transformation [Cas01], qui est un élément de Jonquières. Quand $n \ge 3$ il n'y a pas d'analogue du théorème de Nœther-Castelnuovo, et on ne connait aucun ensemble raisonnable de générateurs de $Bir(\mathbb{P}^n)$. Voici un extrait de l'article “Cremona group” in the Encyclopedia of Mathematics, écrit par V. Iskovskikh en 1987 :

"One of the most difficult problems in birational geometry is that of describing the structure of the group Bir$(\mathbb{P}^3)$, which is no longer generated by the quadratic transformations. Almost all literature on Cremona transformations of three-dimensional space is devoted to concrete examples of such transformations. Finally, practically nothing is known about the structure of the Cremona group for spaces of dimension higher than $3$." [Isk87]

Une question naturelle (posée par exemple dans [PS15]) est de savoir si $Bir(\mathbb{P}^n)$ est engendré par $Aut(\mathbb{P}^n)$ et le groupe des éléments de Jonquières. Une autre question ancienne sur le groupe de Cremona est la suivante: le groupe $Bir(\mathbb{P}^n)$ est-il simple? C'est-à-dire, contient-il des sous-groupes distingués non-triviaux et propres ? La question se trouve déjà dans l'œuvre de F. Enriques :

"Tuttavia altre questioni d'indole gruppale relative al gruppo Cremona nel piano $($ed a più forte ragione in $S_n$ $n>2)$ rimangono ancora insolute; ad esempio l'importante questione se il gruppo Cremona contenga alcun sottogruppo invariante $($questione alla quale sembra probabile si debba rispondere negativamente$)$." [Enr95, p.116]1

En dimension $n = 2$, une réponse a été apportée depuis une dizaine d'années :

Théorème 1 [CL13]. Le groupe de Cremona $Bir(\mathbb{P}^2)$ n'est pas simple.

La stratégie de preuve est d'utiliser l'action de $Bir(\mathbb{P}^2)$ par isométries sur un espace hyperbolique de dimension infinie, puis d'adapter la théorie de petite simplification pour détecter l'existence d'éléments de $Bir(\mathbb{P}^2)$ engendrant un sous-groupe distingué propre. Cette démonstration semble difficilement généralisable pour $n\geq3$, car la construction de l'espace hyperbolique de dimension infinie repose sur la forme d'intersection entre diviseurs qui est particulière au cas des surfaces.

Quotienter $Bir(\mathbb{P}^n)$ par un sous-groupe distingué $N$ induit un morphisme de groupes $Bir(\mathbb{P}^n)\to Bir(\mathbb{P}^n)/N$. Ainsi, construire un sous-groupe distingué dans $Bir(\mathbb{P}^n)$ équivaut à construire un morphisme de groupes de $Bir(\mathbb{P}^n)$ vers un autre groupe. Les groupes distingués détectés dans  le théorème 1 sont très grands, mais aussi leurs quotients, car par exemple le groupe des éléments de Jonquières $PGL_2(\mathbb{C}(x_2))\rtimes PGL_2(\mathbb{C})$ se plonge dedans. En fait il n'existe pas de quotient fini, ou abélien, du groupe $Bir(\mathbb{P}^2)$. Comme nous allons le voir maintenant l'histoire est bien différente en dimension plus grande.

Considérons le morphisme de groupes suivant :

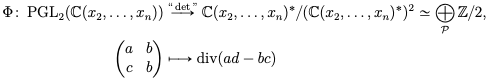
où $\mathcal{P}$ est l'ensemble des hypersurfaces irréductibles dans $\mathbb{P}^{n-1}$. On ne peut pas étendre directement $\Phi$ au groupe de Cremona, mais cela devient possible après projection sur un sous-groupe de $\bigoplus_{\mathcal{P}}\mathbb{Z}/2$:

Théorème 2 [BLZ19]. Pour tout $n\geq3$ il existe un morphisme $Bir(\mathbb{P}^n)\to \bigoplus_{I} \mathbb{Z}/2$ où l'ensemble $I$ est non-dénombrable, tel que la restriction au groupe des dilatations

est surjective. En particulier, le groupe de Cremona $Bir(\mathbb{P}^n)$ n'est pas simple.

Le théorème précédent utilise le fait que $\mathbb{P}^n$ est birationnel au produit $\mathbb{P}^1 \times \mathbb{P}^{n-1}$, sur lequel on comprend explicitement l'action des dilatations, même si l'extension de $\Phi$ au groupe entier est bien moins explicite. Il est possible d'appliquer la même stratégie en utilisant d'autres fibrations de base $\mathbb{P}^{n-1}$, toujours à fibre générale isomorphe à $\mathbb{P}^1$ mais non birationnelles à un simple produit. Le noyau des morphismes vers $\mathbb{Z}/2$ ainsi produits contient les applications de Jonquières, et on en déduit le résultat suivant :

Théorème 3 [BLZ19]. Soit $n\geq3$, $S$ un sous-ensemble dénombrable d'éléments de $Bir(\mathbb{P}^n)$, et soit $G$ le groupe engendré par $Aut(\mathbb{P}^n), PGL_2(\mathbb{C}(x_1,\dots,x_n))\rtimes Bir(\mathbb{P}^{n-1})$ et $S$. Il existe un morphisme surjectif
$$
Bir(\mathbb{P}^n)\to\mathbb{Z}/2
$$
dont le noyau contient $G$. En particulier, $G$ est un sous-groupe propre de $Bir(\mathbb{P}^n)$, ainsi que le sous-groupe distingué engendré par $G$.

En particulier, la réponse à la question de [PS15] est négative : les transformations linéaires et de Jonquières ne suffisent pas à engendrer $Bir(\mathbb{P}^n)$. 

Mais comment construire le morphisme $Bir(\mathbb{P}^n)\to\bigoplus_I \mathbb{Z}/2$ du théorème 2 ?

L'idée de base s'explique déjà sur l'exemple du groupe symétrique $sym_n$.
Ce groupe est engendré par les transpositions $\tau_i=(i\ i+1)$, $i=1,\dots,n-1$, et une présentation du groupe est
$$
Sym_n=\langle \tau_1,\dots,\tau_n\mid \tau_i^2=1,\ (\tau_{i+1}\tau_i)^3=1, \ \tau_i\tau_j=\tau_j\tau_i, |i-j|>2\ \rangle
$$
Le morphisme signature $sym_n\to \{+1,-1\}$ est défini par $\tau_i\mapsto -1$, $i=1,\dots,n-1$. Le fait que cette application soit bien définie et qu'elle soit un morphisme découle de l'observation que chaque relation étant de longueur paire est envoyée sur le neutre. On peut retenir ce principe : pour définir un morphisme d'un groupe vers $\mathbb{Z}/2$, il « suffit » de disposer d'une présentation par générateurs et relations, d'envoyer certains des générateurs sur le générateur de $\mathbb{Z}/2$, et de vérifier que chaque relation est envoyée sur l'élément neutre. A priori cette stratégie paraît difficile à implémenter pour le groupe de Cremona, vu qu'on ne connaît pas d'ensemble de générateurs raisonnables, sans même parler des relations. Nous expliquons maintenant comment nous contournons ce problème, en plongeant $Bir(\mathbb{P}^n)$ dans un groupoïde $BirMori(\mathbb{P}^n)$ encore plus gros, mais pour lequel on disposera d'une présentation par générateurs et relations géométriquement naturelle. On pourra ainsi construire un morphisme vers une somme directe de $\mathbb{Z}/2$, et finalement obtenir le morphisme du théorème 2 par restriction :

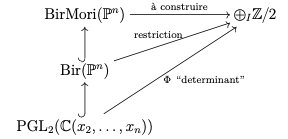
Pour construire le groupoïde, commençons par rappeler que pour tout élément $\mathbb{P}^n$ du groupe de Cremona, il existe une résolution

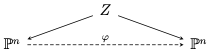
où $Z$ est une variété lisse et les $Z\to\mathbb{P}^n$ sont des morphismes birationnels. Depuis $Z$ on peut lancer le Programme des Modèles Minimaux (MMP) : on contracte peu-à-peu des familles de courbes dont l'intersection contre le diviseur canonique est négative. Le résultat du programme, dans notre cas, est une variété $X$ de dimension $n$ sur laquelle on ne peut plus rien contracter sans chuter en dimension. Elle n'est pas trop singulière, est munie d'un morphisme $X\to B$ où $\dim B<n$, et l'intersection de toute courbe contenue dans toute fibre est négative contre le diviseur canonique. Une telle fibration, notée $X/B$, est appelée une fibration de Mori.

$BirMori(\mathbb{P}^n)$ est le groupoïde des transformations birationnelles entre fibrations de Mori rationnelles. Vu que $\mathbb{P}^n\to \ast$ est une fibration de Mori, le groupe de Cremona $Bir(\mathbb{P}^n)$ est contenu dans $BirMori(\mathbb{P}^n)$.

Géométriquement, toutes les étapes possibles d'un MMP depuis $Z$ sont encodées dans un éventail $\mathcal{C}$ qui se trouve dans l'espace vectoriel $N^1(Z)\otimes\mathbb{R}$, où $N^1(Z)$ est le groupe des diviseurs de $Z$ à équivalence numérique près :

• Un pas du MMP correspond à sauter d'une chambre maximal de l'éventail $\mathcal{C}$  à une autre chambre maximale, en se rapprochant du bord.
• Une fibration de Mori $X_i/B_i$ (le résultat final d'un MMP) correspond à une face $\mathcal{F}^1_i$ de codimension $1$ dans le bord $\partial\mathcal{C}$ de l'éventail $\mathcal{C}$.
• Passer d'une telle face $\mathcal{F}_i^1$ vers une autre, disons $\mathcal{F}_j^1$, en traversant une face $\mathcal{F}^2$ de codimension $2$ correspond à une transformation birationnelle 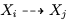, qui s'appelle un lien de Sarkisov.
• Une face $\mathcal{F}^3$ de codimension $3$ dans $\partial\mathcal{C}$ appartient à un nombre fini de faces $\mathcal{F}_1^1,\dots,\mathcal{F}_t^1$ - correspondant aux fibrations de Mori $X_1/B_1,\dots,X_t/B_t$ - dont chacune touche seulement deux autres qui contiennent $\mathcal{F}^3$.

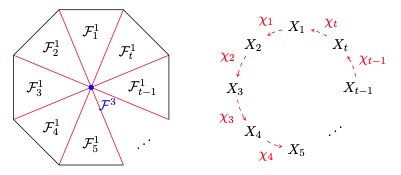
Ainsi $\mathcal{F}^3$ correspond à une relation entre liens de Sarkisov, dite relation élémentaire,
\[\chi_t\circ\cdots\circ\chi_1=\mathrm{id}\]
où $\chi_i$ correspond à la face de codimension $2$ entre $\mathcal{F}^1_i$ et $\mathcal{F}_{i+1}^1$ (et $\mathcal{F}_{t+1}^1=\mathcal{F}_1^1$).

L'ensemble des liens Sarkisov est un ensemble de générateurs du groupoïde $BirMori(\mathbb{P}^n)$ [HM13] ([Cor95] pour $n=2,3$ et [Isk96] pour $n=2$). De plus la géométrie de l'éventail implique que toute relation dans $BirMori(\mathbb{P}^n)$ est engendrée par des relations élémentaires [BLZ19]. On a donc une présentation de notre groupoïde par générateurs et relations :
\[
BirMori(\mathbb{P}^n)=\langle\ \text{liens de Sarkisov}\mid\text{relations élémentaires}\ \rangle.
\]
Maintenant, on peut passer à la construction du morphisme $BirMori(\mathbb{P}^n)\to\oplus_{I}\mathbb{Z}/2$ qui se restreindra en le morphisme $Bir(\mathbb{P}^n)\to\oplus_I\mathbb{Z}/2$ du théorème 2.

Chaque dilatation

préserve une fibration en coniques au-dessus de $\mathbb{P}^{n-1}$, et contracte une hypersurface birationnelle à $\mathbb{P}^1\times\Gamma$, où $\Gamma\subset\mathbb{P}^{n-1}$ est d'équation $\alpha=0$. Considérons une décomposition
\[\phi_{\alpha}=\chi_s\circ\cdots\chi_1\]
en liens de Sarkisov $\chi_1,\dots,\chi_s$.
On se concentre sur les liens de Sarkisov  qui ont des propriétés similaires à $\phi_{\alpha}$:
$B_i=B_{i+1}$ est de dimension $n-1$, et on a un diagramme commutatif

Un tel lien $\chi_i$ préserve la fibration au-dessus de $B_i$ et contracte une hypersurface irréductible birationnelle à $\mathbb{P}^1\times \Gamma_i$, où $\Gamma_i\subset B_i$ est une hypersurface [BLZ19]. Introduisons maintenant une mesure de l'irrationalité de $\Gamma_i$. La gonalité $gon(C)$ d'une courbe de $C$ est définie comme le degré des extensions des corps de fonctions $gon(C):=[\mathbb{C}(C):\mathbb{C}(t)]$.
Autrement dit, $gon(C)$ est le degré minimal des applications rationnelles dominantes . La courbe $C$ est rationnelle si et seulement si $gon(C)=1$. La gonalité d'une courbe hyperelliptique est $2$.
Pour une courbe lisse $C\subset\mathbb{P}^2$ de degré $>1$ la gonalité satisfait $gon(C)=\deg(C)-1$. On appelle gonalité couvrante (covering gonality) $cov.gon(\Gamma_i)$ de $\Gamma_i$ le plus petit entier $c\geq1$ tel que par tout point $x$ d'un ouvert dense de $\Gamma_i$ il passe une courbe $C\subset\Gamma_i$ de gonalité $gon(C)=c$. La propriété $cov.gon(\Gamma_i)=1$ correspond par exemple à la propriété classique d'être uniréglée. Si $\Gamma_i$ est de degré $d\geq n+1$ et possède seulement des singularités canoniques, alors $cov.gon(\Gamma_i)\geq d-n$ [BDE⁺17].

Proposition 4 [BLZ19]. Soit $n\geq3$. Il existe $d_n\geq1$ qui dépend seulement de $n$, tel que : si $\chi_0$ est un liens de Sarkisov dans $BirMori(\mathbb{P}^n)$ de forme (*) qui apparaît dans une relation élémentaire et qui contracte une hypersurface birationnelle à $\mathbb{P}^1\times\Gamma_0$, alors

• ou bien, à permutation cyclique près, la relation élémentaire est de la forme

\[\chi_3\circ\chi_2\circ\chi_1\circ\chi_0= id\]
et $cov.gon(\Gamma_0) = cov.gon(\Gamma_2) \ge d_n$,

• ou bien $cov.gon(\Gamma_0)< d_n$.

La constante $d_n$ dans la proposition 4 provient de la finitude des variétés Fano à singularités contrôlées, résultat obtenu par C. Birkar [Bir19, Bir21].

Nous pouvons finalement construire le morphisme $BirMori(\mathbb{P}^n)\to\oplus_{I}\mathbb{Z}/2$ du théorème 2. Soit  un lien de Sarkisov entre fibrations de Mori $X/B$ et $X'/B'$.

• S'il existe des diagrammes commutatifs de transformations birationnelles

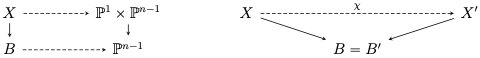
où $\dim B=n-1$ et $\chi$ contracte une hypersurface birationnelle à $\mathbb{P}^1\times\Gamma$ tel que $cov.gon(\Gamma)\ge d_n$, on envoie $\chi$ sur le générateur correspondant à $\Gamma$.

• On envoie tout autre lien de Sarkisov sur zéro.

Par la proposition 4, toute relation élémentaire est envoyée sur le neutre, ce qui assure que notre définition au niveau des liens de Sarkisov s'étend en un morphisme $BirMori(\mathbb{P}^n)\to\oplus\mathbb{Z}/2$. Nous sommes en fait vraiment intéressés à définir un morphisme sur le groupe de Cremona, donc nous considérons la restriction à $Bir(\mathbb{P}^n)$, et il reste à nous assurer que cette restriction n'est pas le morphisme trivial... Heureusement en restriction au sous-groupe des dilatations la construction devient suffisamment explicite pour que l'on puisse vérifier qu'elle correspond bien au morphisme $\Phi$ « déterminant » de la page 2, en tronquant la somme aux hypersurfaces $\Gamma$ vérifiant $cov.gon(\Gamma) \ge d_n$. Notre morphisme est donc déjà surjectif au niveau des dilatations, il est donc bien non trivial sur le groupe de Cremona entier : tout notre travail n'a pas été en vain !

Remerciements

Je remercie Stéphane Lamy pour son fort soutien stylistique et linguistique dans l'écriture de ce texte.

• 1“However, other group-theoretic questions related to the Cremona group of the plane (and, even more so, of ℙn, n>2) remain unsolved; for example, the important question of whether the Cremona group contains any normal subgroup (a question which seems likely to be answered negatively).”