Partitionner des données corrompues, à l'aide de divergences de Bregman

1. Motivation

Diverses questions, par exemple celles des types en anthropologie, ou bien d'autres, d'ordre pratique, comme celles de la normalisation des objets industriels, exigent pour leur solution la détermination de $n$ représentants fictifs d'une nombreuse population, choisis de manière à réduire autant que possible les écarts entre les éléments de la population et ceux de l'échantillon, l'écart étant mesuré entre tout élément réel et l'élément fictif qui lui est le plus proche.

Sur la division des corps matériels en parties, 1956 par H. STEINHAUS, [15]

1.1 Partitionner une population à l'aide de l'algorithme de Lloyd

Si construire des groupes à partir d'une population d'individus ou d'objets par exemple était déjà d'actualité en 1956, elle le demeure toujours. L'utilisation des outils numériques fournit une quantité massive de données que l'on peut chercher à interpréter, notamment en les regroupant judicieusement suivant un critère préalablement défini. Souvent, les données peuvent être assimilées à des points de l'espace Euclidien $\mathbb{R}^{d}$. Partitionner ces données consiste alors à former $k$ groupes disjoints sur la base d'un critère et à associer un représentant (ou centre) à chacun de ces groupes. On appelle dictionnaire un vecteur de $k$ représentants.

Une méthode de partitionnement classique est la méthode des $k$-means de MacQueen de 1967 [11] qui repose sur les idées de Steinhaus [15]. Étant donné un nuage de points $\mathbb{X} = \{X_1, X_2,\ldots, X_n\}$ dans $\mathbb{R}^d$, le critère des $k$-means est défini pour tout dictionnaire $\textbf{c} = (c_1,c_2,\ldots,c_k)$ de $k$ points dans $\mathbb{R}^d$ par [Note 1] : \[ R_n(\textbf{c},\mathbb{X}) = \frac1n\sum_{i=1}^n\min_{c\in\textbf{c}}\|X_i-c\|^2. \]

Le célèbre algorithme de Stuart Lloyd [10] (découvert en 1957, publié en 1982) permet de trouver une solution approchée au problème de minimisation du critère $R_n(\cdot\mathbb{X})$. Cet algorithme, illustré par la Figure 1, fonctionne de la façon suivante. On part d'un dictionnaire de représentants $c_1$, $c_2$,$\ldots$ $c_k$, tirés par exemple uniformément au hasard dans la population. On répète ensuite les deux étapes suivantes, jusqu'à ce que les représentants ne soient plus modifiés :

• On décompose la population en cellules de Voronoï, c'est-à-dire qu'on associe chaque individu (chaque point) au représentant qui lui est le plus proche (en terme de distance Euclidienne)
• On met à jour les représentants en remplaçant chaque représentant par le barycentre des points qui viennent de lui être assignés.

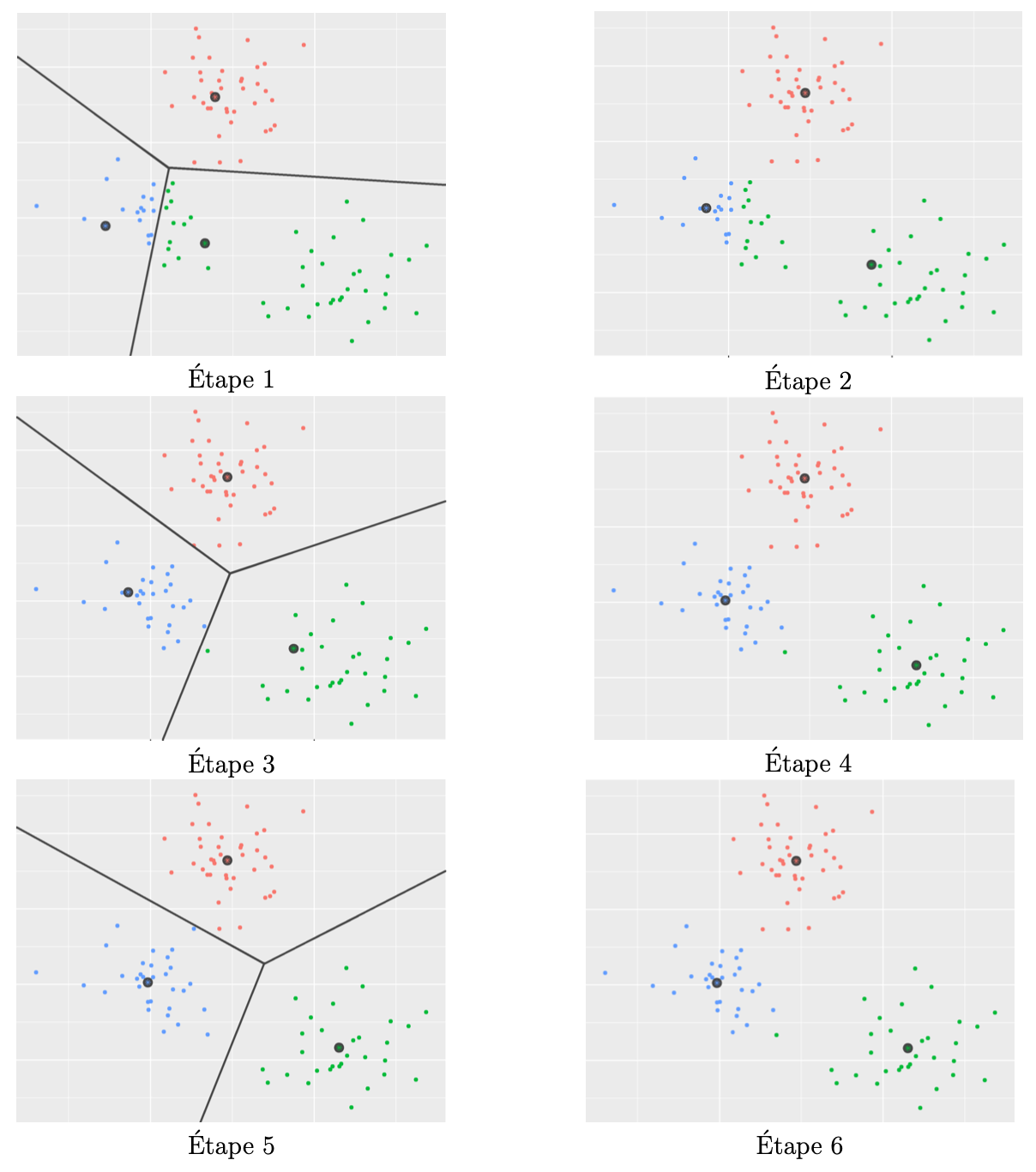
Cette méthode est connue pour fonctionner pour des données naturellement séparées en des groupes isotropes (même comportement dans toutes les directions à partir d'un centre) et de « diamètres » similaires.

Les raisons intrinsèques de la décroissance du critère $R_n(\textbf{c},\mathbb{X})$ à chacune des étapes de l'algorithme de Lloyd, assurant donc la convergence du dictionnaire $\textbf{c}$ vers un minimum local du critère des $k$-means, tient au fait que la fonction $c\mapsto\frac1n\sum_{i=1}^n\|X_i-c\|^2$ est minimale en $c = \frac{1}{n}\sum_{i = 1}^nX_i$. En pratique, il est possible d'atteindre le minimum global du critère $R_n(\cdot,\mathbb{X})$ après plusieurs initialisations de l'algorithme et en gardant le meilleur dictionnaire, celui pour lequel le critère est le plus faible en sortie d'algorithme.

1.2 Un lien avec le transport optimal

Si le critère des $k$-means semble être défini pour des nuages de points, il peut très aisément être généralisé à $\mathcal{P}_2(\mathbb{R}^d)$, l'ensemble des mesures boréliennes de probabilité sur $\mathbb{R}^d$, avec un moment d'ordre 2 fini. Avec la notation $Pf$ ou $Pf(\cdot)$ pour $\int f(x)d P(x)$, l'espérance d'une fonction $f$ intégrable par rapport à la mesure de probabilité $P$, on peut définir le critère des $k$-means par : \[ R:(\textbf{c},P)\in\mathbb{R}^{d\times k}\times\mathcal{P}_2(\mathbb{R}^d)\mapsto P\min_{c\in\textbf{c}}\|c-\cdot\|^2. \] On retrouve le critère empirique $R_n$ lorsque l'on remplace $P$ par la mesure empirique [Note 2] sur $\mathbb{X}$.

Pour rappel, la distance de Wasserstein entre deux mesures $P,Q\in\mathcal{P}_2(\mathbb{R}^d)$ est le coût quadratique moyen minimal pour transporter la mesure $P$ sur la mesure $Q$, [17]. Cette métrique est définie par : \[ W_2(P,Q) = \sqrt{\inf_{\mathcal{L}((X,Y))\mid X\sim P, Y\sim Q}\mathbb{E}\left[\|X-Y\|^2\right]}, \] où l'espérance $\mathbb{E}$ est calculée selon la loi du couple $(X,Y)$, et où l'infimum est pris sur toutes les lois possibles du couple $(X,Y)$ de variables aléatoires où $X$ suit la loi $P$ et $Y$ la loi $Q$.

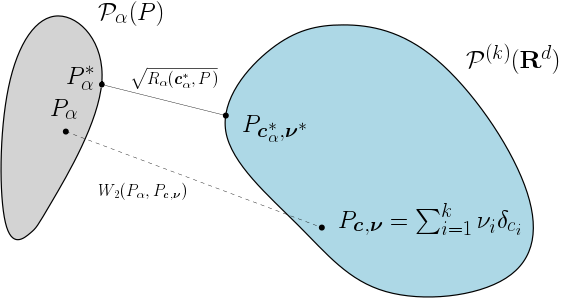
Chercher à minimiser le critère des $k$-means revient en fait à chercher la projection de la mesure $P$, au sens de la distance de Wasserstein, sur $\mathcal{P}^{(k)}(\mathbb{R}^d)$, l'espace des mesures de probabilité sur $\mathbb{R}^d$ dont le support [Note 3] est de cardinal fini, inférieur ou égal à $k$. En effet, \[ W_2^2(P,\mathcal{P}^{(k)}(\mathbb{R}^d)) = \inf_{\textbf{c}}R(\textbf{c},P). \] Ce résultat [Note 4] est représenté par la Figure 4, où les éléments de $\mathcal{P}^{(k)}(\mathbb{R}^d)$ sont les mesures $P_{\textbf{c}, \bf \nu} = \sum_{i = 1}^k\nu_i\delta_{c_i}$, avec $\nu = (\nu_1,\nu_2,\ldots,\nu_k)\in[0,1]^k$ tel que $\sum_{i = 1}^k\nu_i = 1$ et $\textbf{c} = (c_1,c_2,\ldots,c_k)\in\mathbb{R}^{d\times k}$.

Le dictionnaire $\textbf{c}^*$ minimisant le critère des $k$-means correspond au support de la projection de $P$ sur $\mathcal{P}^{(k)}(\mathbb{R}^d)$. Par ailleurs, les poids $\nu^*$ associés aux $k$ points du support sont les masses, calculées selon la mesure $P$, de leurs cellules de Voronoï ($V_1(\textbf{c}^{*}), V_2(\textbf{c}^{*}),\ldots, V_k(\textbf{c}^{*})$).

Naturellement, la perte optimale $R(\textbf{c}^*,P) = W_2^2(P,\mathcal{P}^{(k)}(\mathbb{R}^d))$ est nulle lorsque le support de $P$ possède au plus $k$ points.

1.3 Une généralisation immédiate aux divergences de Bregman

Les divergences de Bregman sont des mesures de distorsion, à savoir, des fonctions de deux variables, à valeur dans $\mathbb{R}_+$. Elles fournissent une façon de mesurer la différence entre les deux variables. Cette mesure est déterminée par le choix d'une fonction convexe.

Les divergences de Bregman ont été introduites par Bregman [6].

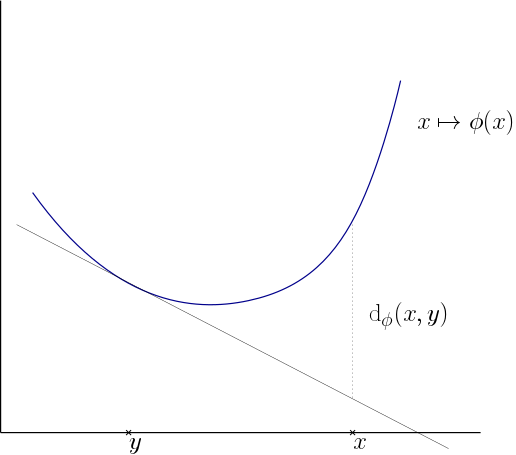
Soit $\phi$, une fonction strictement convexe et $\mathcal{C}^1$ à valeurs réelles, définie sur un sous ensemble convexe $\Omega$ de $\mathbb{R}^d$. La divergence de Bregman associée à la fonction $\phi$ est la fonction $\mathrm{d}_\phi$ définie sur $\Omega\times\Omega$ par : \[\forall x,y\in\Omega,\,{\rm d\it}_\phi(x,y) = \phi(x) - \phi(y) - \langle\nabla\phi(y),x-y\rangle.\]

La divergence de Bregman associée au carré de la norme Euclidienne, $\phi:x\in\mathbb{R}^d\mapsto\|x\|^2\in\mathbb{R}$ est par exemple égale au carré de la distance Euclidienne : \[\forall x,y\in\mathbb{R}^d, {\rm d\it}_\phi(x,y) = \|x-y\|^2.\]

De nombreuses autres divergences de Bregman sont connues et fréquemment utilisées en statistiques comme, par exemple, la divergence de Kullback-Leibler, les carrés des distances de Mahalanobis et des distances $L_2$. La Figure 3 représente le calcul d'une divergence de Bregman en dimension 1 à partir du graphe de la fonction convexe $\phi$.

D'après Banerjee [1], comme le carré de la norme Euclidienne, les divergences de Bregman satisfont la propriété suivante, clé pour le fonctionnement de l'algorithme de Lloyd. \[ \text{ La fonction }c\mapsto\frac1n\sum_{i=1}^n\mathrm{d}_\phi(X_i,c)\text{ est minimale en }c = \frac{1}{n}\sum_{i = 1}^nX_i. \] De façon plus générale, pour tout mesure $Q\in\mathcal{P}_2(\Omega)$, la fonction $c\mapsto Q\mathrm{d}_{\phi}(\cdot,c)$ est minimale en l'espérance de $Q$. [Note 5] Les divergences de Bregman sont d'ailleurs les seules divergences à vérifier cette propriété [Note 6]. En ce sens, l'algorithme de Lloyd est adapté aux divergences de Bregman et seulement aux divergences de Bregman.

Ces considérations ont poussé Banerjee et ses co-auteurs [2] à étudier, en 2005, une variation de la méthode des $k$-means en remplaçant le carré de la norme Euclidienne par une divergence de Bregman quelconque. Cette méthode permet de mieux tenir compte d'éventuelles distorsions dans les données. En particulier, elle est tout-à-fait adaptée à des données échantillonnées selon un mélange [Note 7] de mesures de probabilités issues d'une famille exponentielle. Les familles exponentielles sont des familles de lois déterminées par le choix d'une fonction convexe propre et fermée $\psi$ définie sur un espace paramétrique ouvert $\Theta\subset\mathbb{R}^d$. Les lois, paramétrées par $\theta\in\Theta$, sont de densité de Radon-Nikodym $x\mapsto\exp\left(\langle x,\theta\rangle - \psi(\theta)\right)$ par rapport à une distribution de probabilité $P_0$, et d'espérance $\mu(\theta) = \nabla_\theta\psi$. Par ailleurs, par dualité de Legendre, en posant   $\phi(\mu) = \sup_{\theta\in\Theta}\left\{\langle\mu,\theta\rangle - \psi(\theta)\right\}$, la densité s'exprime à partir d'une divergence de Bregman sous la forme : \begin{equation} p:x\in\Omega\mapsto\exp(-\mathrm{d}_\phi(x,\mu))f(x), \quad (1) \end{equation}

où $\mu$ est l'espérance de la loi et $f$ est une fonction positive, [2]. Les lois normales avec une matrice de covariance fixée ou les lois Gamma en sont des exemples. Par ailleurs, la méthode est aussi adaptée à des familles de lois discrètes dont la fonction de probabilité $p(x)$ satisfait (1). C'est par exemple le cas des lois de Poisson et des lois binomiales.

1.4 Seuiller pour évacuer les données aberrantes

En 1997, dans [8], Cuesta-Albertos et ses co-auteurs ont défini et étudié une version seuillée du critère des $k$-means. Cette version vise à retirer d'un nuage de points une certaine proportion $1-\alpha\in]0,1[$ des données. Il s'agit de points considérés comme des données aberrantes, car trop éloignés de leur centre.

La version $\alpha$-seuillée du risque empirique est définie par : \[ R_{n,\alpha}:(\textbf{c},\mathbb{X})\in\mathbb{R}^{d\times k}\times\mathbb{R}^{d\times n}\mapsto\inf_{\mathbb{X}_\alpha\subset \mathbb{X}, |\mathbb{X}_\alpha| = a}R_n(\textbf{c},\mathbb{X}_\alpha), \] avec $a = \lceil\alpha n\rceil$, la partie entière supérieure de $\alpha n$, et \(|\mathbb{X}_\alpha|\) le cardinal de  \(\mathbb{X}_\alpha\).

Minimiser le risque empirique $\alpha$-seuillé $R_{n,\alpha}(\cdot,\mathbb{X})$ revient à sélectionner le sous-ensemble de $\mathbb{X}$ de $a$ points pour lequel le critère empirique optimal est le plus faible, c'est-à-dire, le sous-ensemble le mieux représenté par $k$ centres. À dictionnaire fixé, il s'agit de la restriction de $\mathbb{X}$ à une union de boules de même rayon, centrées en les centres du dictionnaire.

Ajouter une étape à l'algorithme de Lloyd permet de calculer un minimum local du critère $R_{n,\alpha}(\cdot,\mathbb{X})$. Voici la procédure. On part d'un dictionnaire de représentants $c_1$, $c_2$,$\ldots$ $c_k$, tirés uniformément au hasard dans $\mathbb{X}$. On répète ensuite les trois étapes suivantes, jusqu'à ce que les représentants ne soient plus modifiés :

• On décompose la population en cellules de Voronoï
• On retire les $n - a = n - \lceil\alpha n\rceil$ points les plus loin de leur centre en terme de distance Euclidienne
• On met à jour les représentants en remplaçant chaque représentant par le barycentre des points restant dans sa cellule, puis on recommence la première étape avec tous les points.

La version continue de ce critère s'étend à l'ensemble des mesures boréliennes de probabilité sur $\mathbb{R}^d$, $\mathcal{P}(\mathbb{R}^d)$, sans condition de moment d'ordre 2 fini. Ce critère se définit à partir de sous-mesures, par : \[ R_{\alpha}:(\textbf{c},P)\in\mathbb{R}^{d\times k}\times\mathcal{P}(\mathbb{R}^d)\mapsto\inf_{P_\alpha\in\mathcal{P}(\mathbb{R}^d),\,\alpha P_\alpha\preceq P}R(\textbf{c},P_\alpha), \] où $\alpha P_\alpha\preceq P$ signifie que $\alpha P_\alpha$ est une sous-mesure de $P$. [Note 8] Minimiser le risque seuillé $R_{\alpha}(\cdot,P)$ revient à sélectionner la sous-mesure $\alpha P_\alpha$ de $P$, de masse $\alpha$, pour laquelle le critère optimal $\inf_{\textbf{c}}R(\textbf{c},P_\alpha)$ est le plus faible, ainsi que le dictionnaire optimal associé, $\textbf{c}^*_\alpha$. On note cette sous-mesure optimale $\alpha P^*_\alpha$. Il s'agit de la restriction de la mesure $P$ à une union de boules de mêmes rayons, centrées en les centres de $\textbf{c}^*_\alpha$.

On pourra remarquer qu'il s'agit en fait de chercher deux mesures, l'une dans $\mathcal{P}_\alpha(P) = \{P_\alpha\in\mathcal{P}(\mathbb{R}^d),\,\alpha P_\alpha\preceq P\}$, l'autre dans $\mathcal{P}^{(k)}(\mathbb{R}^d)$, pour lesquelles la distance de Wasserstein est minimale, comme représenté dans la Figure 4. D'après [8, Théorème 3.1], deux telles mesures existent, sans condition de moment d'ordre 2 fini pour la mesure $P$.

2. Une nouvelle méthode de partitionnement robuste avec des divergences de Bregman

Avec Aurélie Fischer et Clément Levrard, dans [4], nous avons étudié la version seuillée du critère des $k$-means avec des divergences de Bregman, faisant le pont entre les travaux de Banerjee et al. [2] et les travaux de Cuesta-Albertos et al. [8].

Étant donnée une divergence de Bregman $\mathrm{d}_\phi$ définie à partir d'une fonction $\phi$ strictement convexe sur un ensemble $\Omega$ convexe de $\mathbb{R}^d$, et $\alpha\in]0,1[$, la version continue du critère $\alpha$-seuillé est définie sur l'espace des mesures boréliennes de probabilité sur $\Omega$, $\mathcal{P}(\Omega)$, par : \[ R_{\phi,\alpha}:(\textbf{c},P)\in\Omega^{k}\times\mathcal{P}(\Omega)\mapsto\inf_{P_\alpha\in\mathcal{P}(\Omega),\,\alpha P_\alpha\preceq P}P_\alpha\min_{c\in\textbf{c}}\mathrm{d}_\phi(c,\cdot). \] On note $R_{n,\phi,\alpha}$ la version discrète du critère où $P$ est remplacée par la mesure empirique. D'après [4, Théorème 8], l'existence de minimiseurs de ces deux critères est assurée sous les conditions suivantes : $P\|\cdot\|<\infty$, $\phi$ est dans $\mathcal{C}^2(\Omega)$ et la fermeture de l'enveloppe convexe du support de $P$ est incluse dans l'intérieur de $\Omega$. On supposera ces conditions vérifiées dans la suite et on note $\textbf{c}_\alpha^*$ un  minimiseur de $R_{\phi,\alpha}(\cdot,P)$, $\hat{\textbf{c}}_{n,\alpha}$ un minimiseur de $R_{n,\phi,\alpha}(\cdot,\mathbb{X})$, pour $\mathbb{X}$ un échantillon de loi $P$ et $R^*_{\phi,k,\alpha} = R_{\phi,\alpha}(\textbf{c}_\alpha^*,P)$.

L'algorithme de Lloyd s'adapte très bien et permet de calculer un minimum local du critère $R_{n,\phi,\alpha}(.,\mathbb{X})$. Il suffit de reprendre l'algorithme de la Section 1.4 et de remplacer distance Euclidienne par divergence de Bregman, et cellule de Voronoï par cellule de Bregman-Voronoï, [13].

2.1 Convergence des dictionnaires empiriques vers un dictionnaire optimal

On s'intéresse maintenant à la convergence des dictionnaires empiriques optimaux vers un dictionnaire optimal, lorsque la taille de l'échantillon croît vers l'infini.

Si $P$ est absolument continue par rapport à la mesure de Lebesgue sur $\mathbb{R}^d$, et si pour un $p>2$, $P\|\cdot\|^p<\infty$, alors il existe un minimiseur $\textbf{c}_{\alpha}^*$ de $R_{\phi,\alpha}(.,P)$ tel que, presque sûrement, $R_{n,\phi,\alpha}(\hat{\textbf{c}}_{n,\alpha},\mathbb{X})$ converge vers $R_{\phi,\alpha}(\textbf{c}_{\alpha}^*,P)$. Par ailleurs, à extraction d'une sous-suite près, $\hat{\textbf{c}}_{n,\alpha}$ converge presque sûrement vers $\textbf{c}_{\alpha}^*$, à permutation des coordonnées près [Note 9]. Sous-hypothèse d'unicité du minimiseur de $R_{\phi,\alpha}(.,P)$, cette convergence a lieu sans hypothèse d'extraction de sous-suite.

Ces résultats permettent d'assurer que les $k$ centres obtenus à partir d'un échantillon de points de loi $P$ vont converger vers les centres optimaux, ainsi que les critères associés. Les résultats suivants [4, Théorème 11, Corollaire 12] donnent la vitesse à laquelle la convergence des critères a lieu. Il s'agit de la vitesse paramétrique en $\frac{1}{\sqrt{n}}$, classique en statistiques.

Pour s'assurer qu'aucune sous-mesure de masse $\alpha$ de $P$ n'est supportée sur $k-1$ points, et donc que le dictionnaire optimal n'est pas réduit à un ensemble de $k-1$ points, on suppose que $R^*_{\phi,k,\alpha} - R^*_{\phi,k-1,\alpha}>0$. On suppose également que pour $p\geq 2$, $P\|\cdot\|^p<\infty$. Alors, pour $n$ assez grand, avec probabilité supérieure à $1 - n^{-\frac{p}{2}} - 2e^{-x}$, \[ R_{\phi,\alpha}(\hat{\textbf{c}}_{n,\alpha},P) - R_{\phi,\alpha}(\textbf{c}_{\alpha}^*,P) \leq \frac{C_P}{\sqrt{n}}(1+\sqrt{x}). \] Sous des hypothèses supplémentaires [Note 10], pour une constante $C_P>0$, \[ \mathbb{E}\left[R_{\phi,\alpha}(\hat{\textbf{c}}_{n,\alpha},P) - R_{\phi,\alpha}(\textbf{c}_{\alpha}^*,P)\right]\leq \frac{C_P}{\sqrt{n}}. \]

2.2 Mesurer la robustesse au bruit

Le bruit antagoniste adversarial noise, en anglais) consiste à ajouter des points $\{x_1,\ldots,x_s\}$ à l'échantillon initial $\mathbb{X}$, de sorte à altérer volontairement certains estimateurs construits à partir de l'échantillon (par exemple, les dictionnaires optimaux $\hat{\textbf{c}}_{n,\alpha}$). Une notion de mesure de robustesse au bruit antagoniste en statistiques est celle de point de rupture (breakdown point, en anglais) [9]. En notant $P_{n+s}$ la mesure empirique, uniforme sur $\mathbb{X}\cup\{x_1,\ldots,x_s\}$ et $\hat{\textbf{c}}_{n+s,\alpha}$ un dictionnaire minimisant le critère $R_{n+s,\phi,\alpha}(.,\mathbb{X})$, le point de rupture est défini par [Note 11] : \[ \hat{{\rm BP}}_{n,\alpha} = \inf\left\{\frac{s}{n+s}\mid \sup_{\{x_1,\ldots,x_s\}}\left\|\hat{\textbf{c}}_{n+s,\alpha}\right\| = \infty\right\}. \] Il s'agit de la proportion minimale de points que l'on s'autorise à ajouter à l'échantillon pour qu'au moins un des centres du dictionnaire optimal soit arbitrairement grand (pour la norme Euclidienne).

Lorsque $k = 1$, le point de rupture de l'estimateur standard de la moyenne est égal à $\frac1{n+1}$. En effet, ajouter un unique point dans l'échantillon, de norme  Euclidienne arbitrairement grande, rend la moyenne de norme Euclidienne arbitrairement grande. Pour $\alpha\in]0,1[$,  le point de rupture de la moyenne seuillée vaut environ $1-\alpha$, [12, Section 3.2.5]. Il est d'autant plus grand (et donc la procédure est d'autant plus robuste) que la proportion de points gardés dans la procédure, $\alpha$, est faible.

En revanche, lorsque l'on cherche plus d'un centre, c'est-à-dire, lorsque $k>1$,  le point de rupture peut être très inférieur à $1-\alpha$, [8]. En effet, un petit groupe de points, éloigné des données initiales, pourra être considéré comme un groupe auquel un centre, de grande norme, sera associé. Si aucun résultat plus précis n'avait été démontré jusqu'alors, voici les résultats obtenus dans [4]. Ils reposent en particulier sur la notion de facteur de perceptibilité (discernability factor, en anglais), qui permet de quantifier l'intuition selon laquelle ajouter un groupe de points antagonistes peut induire un échange des rôles (bruit/signal) de certains points de l'échantillon, par l'allocation d'un centre à ce groupe antagoniste et l'élimination, par seuillage, d'un groupe de points optimal trop petit.

Pour $\alpha\in]0,1[$ et $b\in[0,\alpha]$, en notant $\alpha_b^- = \frac{\alpha-b}{1-b}$ et $\alpha_b^+ = \frac{\alpha}{1-b}$, le facteur de perceptibilité $B_\alpha$ est défini par : \[ B_\alpha = \sup\left\{b\geq 0\mid b\leq\alpha\wedge(1-\alpha)\text{ et }\min_{j\in\{2,3\,\ldots,k\}}R^*_{\phi,j-1,\alpha_b^-}-R^*_{\phi,j,\alpha_b^+}>0\right\}. \] Dès lors qu'aucune sous-mesure de $P$ de masse $\alpha$ n'est supportée sur un ensemble de $k$ points (c'est-à-dire, $R^*_{\phi,k-1,\alpha} - R^*_{\phi,k,\alpha}>0$), $B_\alpha$ est bien défini, car l'ensemble à partir duquel il est défini est non vide. En effet, $b = 0$ en est un élément. Dans ce cas, $B_\alpha>0$. Par ailleurs, le facteur de perceptibilité est majoré par $\frac{p_{j,\alpha}}{1-(\alpha-p_{j,\alpha})}$ où $p_{j,\alpha} = \min_{p\in\{1,2\,\ldots,j\}}P^*_\alpha(V_p(\textbf{c}^{*,(j)}_\alpha))$ représente, pour la sous-mesure optimale $\alpha P^*_\alpha$ associée au dictionnaire optimal $\textbf{c}^{*,(j)}_\alpha$ à $j$ centres, la plus faible masse d'une cellule de Voronoï associée aux $j$ centres.

De façon générale, $\alpha - \alpha^-_{B_\alpha} = \frac{(1-\alpha)B_\alpha}{1-B_\alpha}$ est la portion de masse d'un dictionnaire optimal à $k$ centres pour un seuillage de niveau $\alpha$, qui serait considéré comme du bruit par un dictionnaire optimal à $k-1$ centres pour un seuillage de niveau $\alpha^-_{B_\alpha}$.

Enfin, il est possible de faire le lien entre ce facteur de perceptibilité et le point de rupture. Lorsque $P\|\cdot\|^p<\infty$, pour $p\geq 2$ et que $R^*_{\phi,k-1,\alpha} - R^*_{\phi,k,\alpha}>0$, alors pour tout $b<B_{\alpha}$ et $s\in\mathbb{N}$ tel que $\frac{s}{n+s}\leq b$, pour $n$ assez grand, avec probabilité plus grande que $1 - n^{-\frac p2}$ : \[ \max_{j\in\{1,2\,\ldots,k\}}\mathrm{d}_\phi(B(0,C_{P,b}),\hat c_{n+s,h,j})\leq K_{P,b}, \] où $C_{P,b}$ et $K_{P,b}$ sont deux constantes ne dépendant ni de $n$, ni de $s$.

Par conséquent, si $P\|\cdot\|^p<\infty$ pour $p>2$, presque sûrement, le point de rupture est strictement positif pour $n$ assez grand. Par ailleurs, si pour tout $x\in\Omega$, l'application $c\mapsto\mathrm{d}_\phi(x,c)$ est propre, alors presque sûrement, pour $n$ assez grand : \[ \hat{{\rm BP}}_{n,\alpha} \geq B_\alpha. \]

Ceci garantit la robustesse asymptotique de notre procédure à une certaine proportion de bruit antagoniste.

2.3 Illustration de la méthode, autour de la loi de Poisson

À ce travail est associé un tutoriel ainsi qu'un dépôt Gitlab [3] contenant les fichiers sources pour le tutoriel. Ce tutoriel est disponible ici. Les différentes figures représentées dans la suite sont issues de ce tutoriel. Elles illustrent la méthode en dimension 1, 2 et en dimension supérieure, sur des données simulées puis réelles de loi de Poisson.

La loi de Poisson de paramètre $\lambda\in\mathbb{R}_+^*$ est une loi de probabilité discrète, notée $\mathcal{P}(\lambda)$. Une variable aléatoire $X$ de loi de Poisson $\mathcal{P}(\lambda)$ est à valeurs entières et satisfait : \[ \forall x\in\mathbb{N},\,Pr(X = x) = p(x) = \frac{\lambda^x}{x!}\exp(-\lambda). \] Cette fonction de probabilité est bien du type (1), pour la fonction convexe $\phi: x\in\mathbb{R}_+^*\mapsto x\ln(x) -x \in\mathbb{R}. $ La divergence de Bregman associée, $\mathrm{d}_{\phi}$, est définie pour tous $x,y\in\mathbb{R}_+^*$ par : \[ \mathrm{d}_{\phi}(x,y) = x\ln\left(\frac{x}{y}\right) - (x-y). \]

En dimension plus grande, un vecteur aléatoire $X=(X_1,X_2,\ldots,X_d)$ de $d$ variables aléatoires indépendantes de lois respectives $\mathcal{P}(\lambda_1),\mathcal{P}(\lambda_2),\ldots,\mathcal{P}(\lambda_d)$ a aussi une fonction de probabilité du type (1). La divergence de Bregman correspondante, $d_{\phi_d}$, est associée à la fonction convexe
\[
\phi_d: x\in\left(\mathbb{R}_+^*\right)^d\mapsto \sum_{i = 1}^d\left(x_i\ln(x_i) - x_i\right)\in\mathbb{R},
\]
et est définie pour tous $x,y\in\left(\mathbb{R}_+^*\right)^d$ par :
\[
d_{\phi_d}(x,y) = \sum_{i = 1}^d \left(x_i\ln\left(\frac{x_i}{y_i}\right) - (x_i-y_i)\right).
\]

Dans la suite sont représentés les partitionnements obtenus en utilisant la méthode seuillée avec la divergence de Bregman associée à la loi de Poisson (Méthode 2). Elle est comparée à la méthode standard des $k$-means seuillés [8] qui repose sur le carré de la norme Euclidienne (Méthode 1).

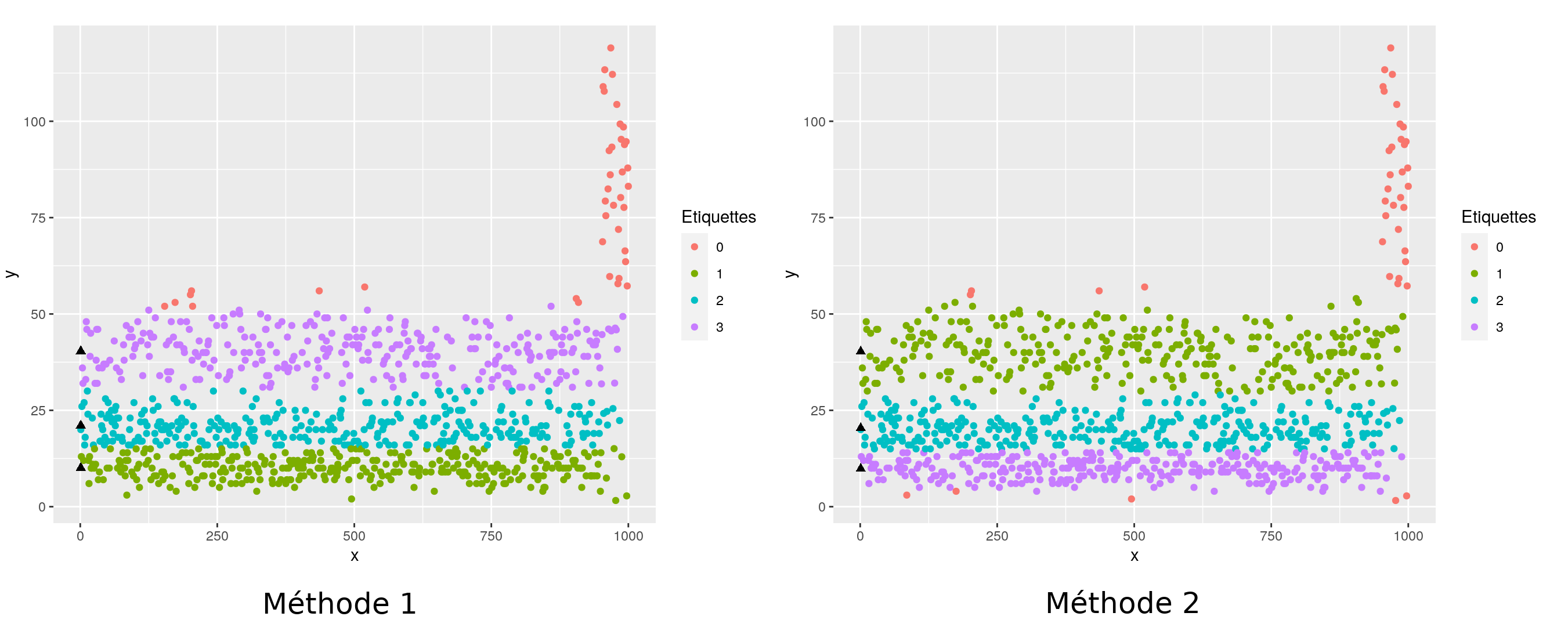
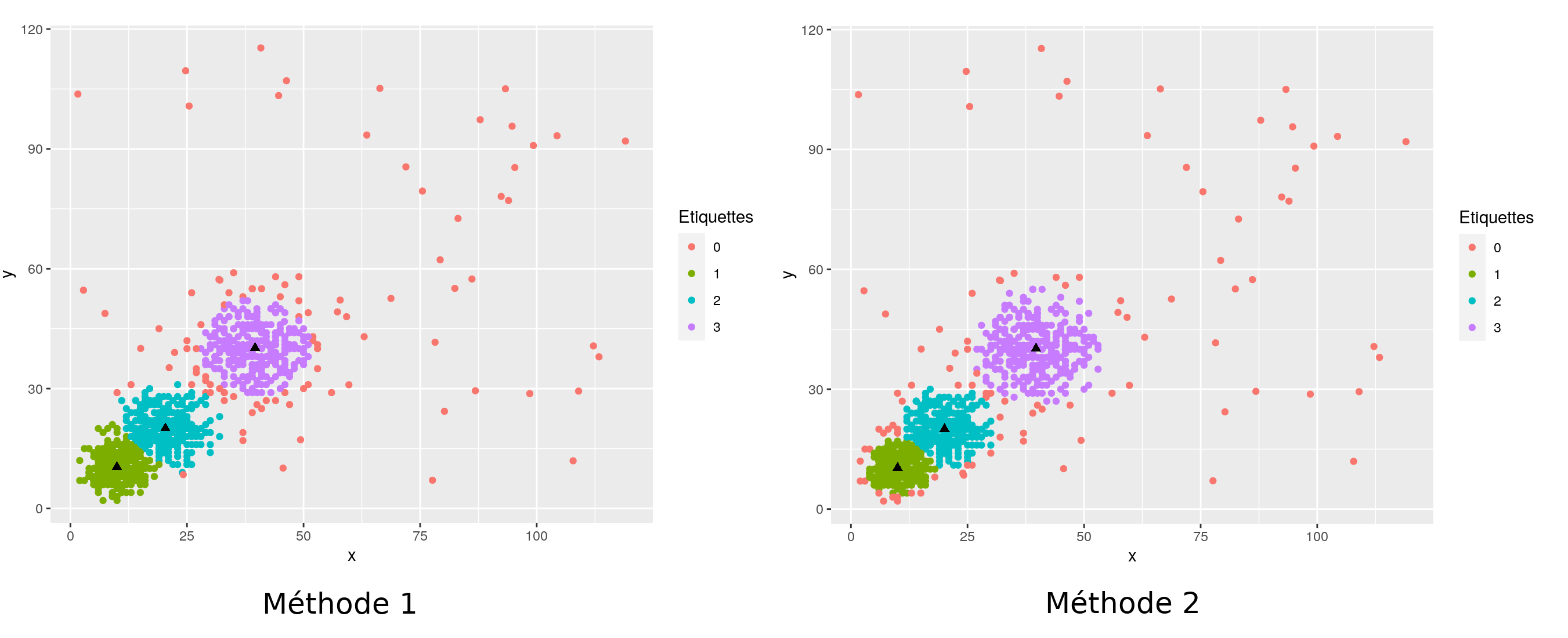
En dimension 1, comme en dimension 2, on voit que le fait d'utiliser la bonne divergence de Bregman permet de s'adapter à la forme des données, en particulier, la largeur des groupes est de plus en plus importante à mesure que le centre (représenté par un triangle plein) est loin de l'origine ($0$ ou $(0,0)$).

Nous présentons maintenant un exemple issu de données réelles, en dimension supérieure. Nous considérons des textes de différents écrivains britanniques (Arthur Conan Doyle, Charles Dickens, Nathaniel Hawthorne et Mark Twain) et de quelques textes issus de la bible ou de discours de Barack Obama [Note 12]. Des passages de longueur 5000 ont été extraits des différents textes. Une liste de 50 mots-clés a été retenue. À chacun des passages est associé un point dans $\mathbb{R}^{50}$. Chacune des coordonnée correspond au nombre d'apparition du mot-clé ou de ses dérivés directs dans le passage.

Il en résulte un nuage de points dans $\mathbb{R}^{50}$. Il est fréquent de modéliser ce type de données par des vecteurs aléatoires dont les coordonnées sont indépendantes, de loi de Poisson. Nous partitionnons ces données en utilisant la divergence de Bregman associée à la loi de Poisson.

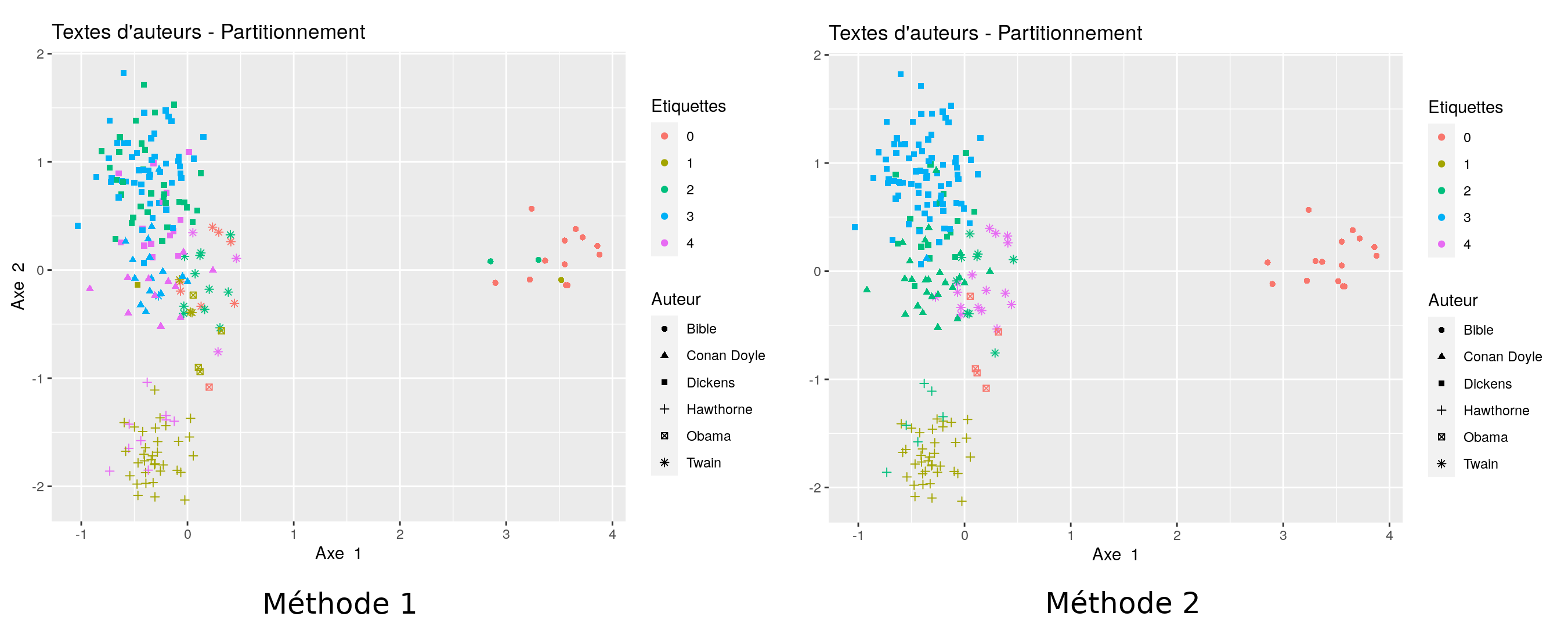
Si le partitionnement n'est pas parfait, les textes de la bible et du discours de Obama sont quand même détectés comme données aberrantes. Une méthode pour sélectionner les paramètres $k$ et $\alpha$ est disponible dans le tutoriel. Dans cet exemple, d'autres choix auraient été possibles. Choisir 6 groupes, sans seuillage fait apparaître deux nouveaux groupes : les textes issus de la bible et les textes issus des discours de Obama.

3. Pour aller plus loin

La méthode proposée ici a des applications par exemple dans le domaine récent de l'analyse topologique des données. En effet, elle permet de construire un proxy (une fonction de substitution) pour la fonction distance à un compact, dont les sous-niveaux sont des unions de boules, [5]. En particulier, en absence du compact, ce proxy [Note 13] peut être estimé à partir de données tirées sur le compact, bruitées. Ceci fournit un estimateur de la fonction distance au compact, robuste à certains types de bruit, dont on peut facilement calculer l'homologie persistance associée (évolution des composantes connexes, boucles, creux etc. dans la filtration [Note 14] des sous-niveaux). Cette méthode repose sur le choix d'une divergence de Bregman dépendante des données, et nécessitant une recherche de plus proches voisins. Seule la version non seuillée a été étudiée sur le plan théorique. Cependant, la version seuillée offre déjà de belles perspectives sur le plan pratique.

Mes remerciements vont à Clément Levrard ainsi qu'à Mehdi Badsi pour leur relecture.

Notes

[Note 1] Étant donné un dictionnaire $\textbf{c} = (c_1,c_2,\ldots,c_k)$ de $k$ points dans $\mathbb{R}^d$, la notation abusive $\min_{c\in\textbf{c}}f(c)$ fait référence à $\min_{i\in\{1,2,\ldots,k\}}f(c_i)$.

[Note 2] La mesure empirique (sur $\mathbb{X}$) est la mesure uniforme sur l'échantillon $\mathbb{X}$ : $P_n = \frac{1}{n}\sum_{i = 1}^n\delta_{X_i}$, où $\delta_{X_i}$ est la mesure de Dirac en le point $X_i$.

[Note 3] Le support d'une mesure $P$ définie sur $\mathbb{R}^d$ est le plus petit fermé $F$, au sens de l'inclusion tel que $P(F) = 1$. On dit que $P$ est supportée sur $F$.

[Note 4] Ce résultat vient de l'écriture $W_2^2(P,\mathcal{P}^{(k)}(\mathbb{R}^d))  = \inf_{\textbf{c},\bf \nu}\inf_{\mathcal{L}((X,Y))\mid X\sim P, Y\sim P_{\textbf{c},\bf \nu}}\mathbb{E}\left[\|X-Y\|^2\right]$. Cette expression devient $\inf_{\textbf{c},\bf \nu}\inf_{P_1,P_2,\ldots,P_k\mid\sum_{i=1}^kP_i = P\text{ et }\forall i, P_i(\mathbb{R}^d)=\nu_i}\sum_{i = 1}^kP_i\|\cdot - c_i\|^2$ en conditionnant par rapport aux valeurs de $Y$. On obtient enfin, en choisissant comme mesures $P_i$ les restrictions de $P$ aux cellules de Voronoï $V_i(\textbf{c})$ des centres $c_i$ : $W_2^2(P,\mathcal{P}^{(k)}(\mathbb{R}^d)) = \inf_{\textbf{c}}\inf_{P_1,P_2,\ldots,P_k\mid\sum_{i=1}^kP_i = P}\sum_{i = 1}^kP_i\min_{c\in\textbf{c}}\|\cdot - c\|^2  = \inf_{\textbf{c}}R(\textbf{c},P)$.

[Note 5] La fonction $c\mapsto Q\mathrm{d}_{\phi}(\cdot,c)$ est minimale en l'espérance de $Q$, notée $Q\cdot$, puisque $Q\mathrm{d}_\phi(\cdot,c)=Q\mathrm{d}_\phi(\cdot,Q\cdot) + \mathrm{d}_\phi(Q\cdot,c)$ et que $\mathrm{d}_\phi(Q\cdot,c)$ est positive [14, Théorème 25.1] et est nulle seulement lorsque $c = Q\cdot$, par stricte convexité de $\phi$.

[Note 6] Les seules fonctionelles $F$ définies sur $\Omega\times\Omega$ telles que pour toute mesure $Q$, $QF(\cdot,c)$ est minimale en $c=Q\cdot$ s'écrivent comme $F_0 + C$ où $C$ est une constante et $F_0$ une divergence de Bregman, [1].

[Note 7] Un mélange de mesures de probabilité $P_1, P_2$,$\ldots,$ $P_k$ est une distribution $P$ du type $P = \sum_{i = 1}^k\nu_i P_i$, où $\sum_{i=1}^k\nu_i = 1$ et $\nu_1$, $\nu_2$,$\ldots,$ $\nu_k\geq 0$. Une variable aléatoire générée selon une telle loi est une variable qui est générée selon la loi $P_i$ avec probabilité $\nu_i$.

[Note 8] Dire que $\alpha P_\alpha$ est une sous-mesure de $P$, c'est dire que $\alpha P_\alpha(B)\leq P(B)$ pour tout borélien $B$ de $\mathbb{R}^d$.

[Note 9] La convergence à lieu au sens de la métrique $D(\textbf{c},\textbf{c}') = \inf_{\sigma\in\Sigma_k}\sup_{i\in\{1,2\,\ldots,k\}}\|c_i-{c'}_{\sigma(i)}\|$, où $\Sigma_k$ est l'ensemble des permutations de l'ensemble $\{1,2\,\ldots,k\}$

[Note 10] On doit supposer l'existence d'une fonction croissante convexe $\psi$ telle que pour tout $t>0$, $\|\nabla_c\phi\|\leq\psi(t)$ en tout point $c$ de la fermeture de l'enveloppe convexe du support de $P$, appartenant à la boule $B(0,t)$. On suppose également que $P\|\cdot\|^p<\infty$ pour un $p\geq 2$ et que pour $q = \frac{p}{p-1}$, $P\|\cdot\|^q\psi^q\left(\frac{k\|\cdot\|}{\alpha}\right)<\infty$.

[Note 11] On s'autorise l'abus de notation $\|\textbf{c}\| = \max_{i\in\{1,2\,\ldots,k\}}\|c_i\|$ pour $\textbf{c} = (c_1,\ldots,c_k)\in\mathbb{R}^{d\times k}$}

[Note 12] La base de données des textes d’auteurs est disponible dans l’appendice de [16]. Les données du discours de Obama sont issues des huit State of the Union Addresses, extraite de la base de données obama de la librairie R CleanNLP. Les données de la bible correspondent à la version de King James. Elles sont disponibles sur Projet Gutenberg.

[Note 13] Lorsque $P\in\mathcal{P}_2(\mathbb{R}^d)$ est une mesure dont le support est le compact d'intérêt, on considère pour $h\in]0,1[$ un paramètre de régularité, la fonction distance à la mesure [7], $\mathrm{d}_{P,h}:x\mapsto\sqrt{\inf_{P_h\in\mathcal{P}_2(\mathbb{R}^d)\mid hP_h \preceq P}P_h\|x-\cdot\|^2}$. Le proxy est le critère $R_{\phi}$ obtenu à partir de la divergence de Bregman associée à la fonction convexe $\phi:x\in\mathbb{R}^d\mapsto||x||^2-d^2_{P,h}(x)$.

[Note 14] Une filtration de parties d'un ensemble $E$ est une famille de sous-ensembles de $E$, $(E_t)_{t\in T}$, indexée par un ensemble ordonné $T$, telle que : $\forall t,t'\in T,\, t\leq t'\Rightarrow E_t\subset E_{t'}$.