Près d’une dynamique stagnante, avec le temps et une loupe, tout peut arriver
Une dynamique est la répétition infinie d’une transformation d’un espace (cercle, sphère ou même notre espace). Celles issues de la physique sont le plus souvent lisses : la transformation y est infiniment dérivable. C’est le cas de l’identité, dynamique qui fixe chaque point. Pierre Berger1 , Nicolas Gourmelon2 et Mathieu Helfter3 viennent de résoudre un problème vieux de 50 ans en démontrant que toute dynamique lisse peut être obtenue en perturbant l’identité, à un changement d’échelles de temps et d’espace près. Leur article, Every diffeomorphism is a total renormalization of a close to identity map, a été publié chez Inventiones mathematicae.
Prenons un disque 𝔻 et appliquons-lui une secousse, de sorte que chaque point x soit envoyé sur un point f(x). Ceci définit une transformation f de 𝔻. Nous pouvons supposer cette transformation continue : deux points proches sont envoyés par la transformation vers deux points proches. Le champ des systèmes dynamique s’intéresse à l’itération d’une telle transformation. On répète exactement la même secousse de sorte que le point x est d’abord envoyé en f(x) , puis en f 2(x) := f (f (x)), puis en f 3(x) := f(f(f(x))), etc. Cela définit une suite infinie de points (f n(x))n appelée orbite de x.
Par exemple, si la secousse est nulle, on a f(x) = x pour x dans le disque 𝔻 et la transformation f est appelée l’identité. La dynamique est alors la plus simple qui soit : toutes les orbites sont constantes. A l’inverse, une secousse violente — donc une transformation éloignée de l’identité — peut engendrer une dynamique difficile à décrire. Qu’en est-il des petites secousses, c’est-à-dire des transformations proches de l’identité ? Sont elles plus simples à décrire ? Il vient d’être démontré que non. Leur dynamique peut-être tout aussi complexe.
En effet Pierre Berger, Nicolas Gourmelon et Mathieu Helfter ont démontré que si on se donne n’importe quelle transformation F du disque 𝔻, et plus précisément n’importe quel difféomorphisme (application infiniment dérivable et inversible), alors il existe une transformation f du disque 𝔻 arbitrairement proche de l’identité et un petit disque D ⊂ 𝔻, tels que si l’on zoome sur D et si l’on accélère la dynamique de f, on voit la dynamique de F. Ici, proche de l’identité signifie que non seulement f(x) est proche de x, mais aussi toutes les dérivées de f sont proches de celles de l’identité. Accélérer la dynamique signifie considérer une itération fN au lieu de f, et Zoomer veut dire observer à travers une « loupe », ou plus précisément à travers un difféomorphisme L agrandissant D en 𝔻. Formellement, cela s’écrit :
F ∘ L = L ∘ fN
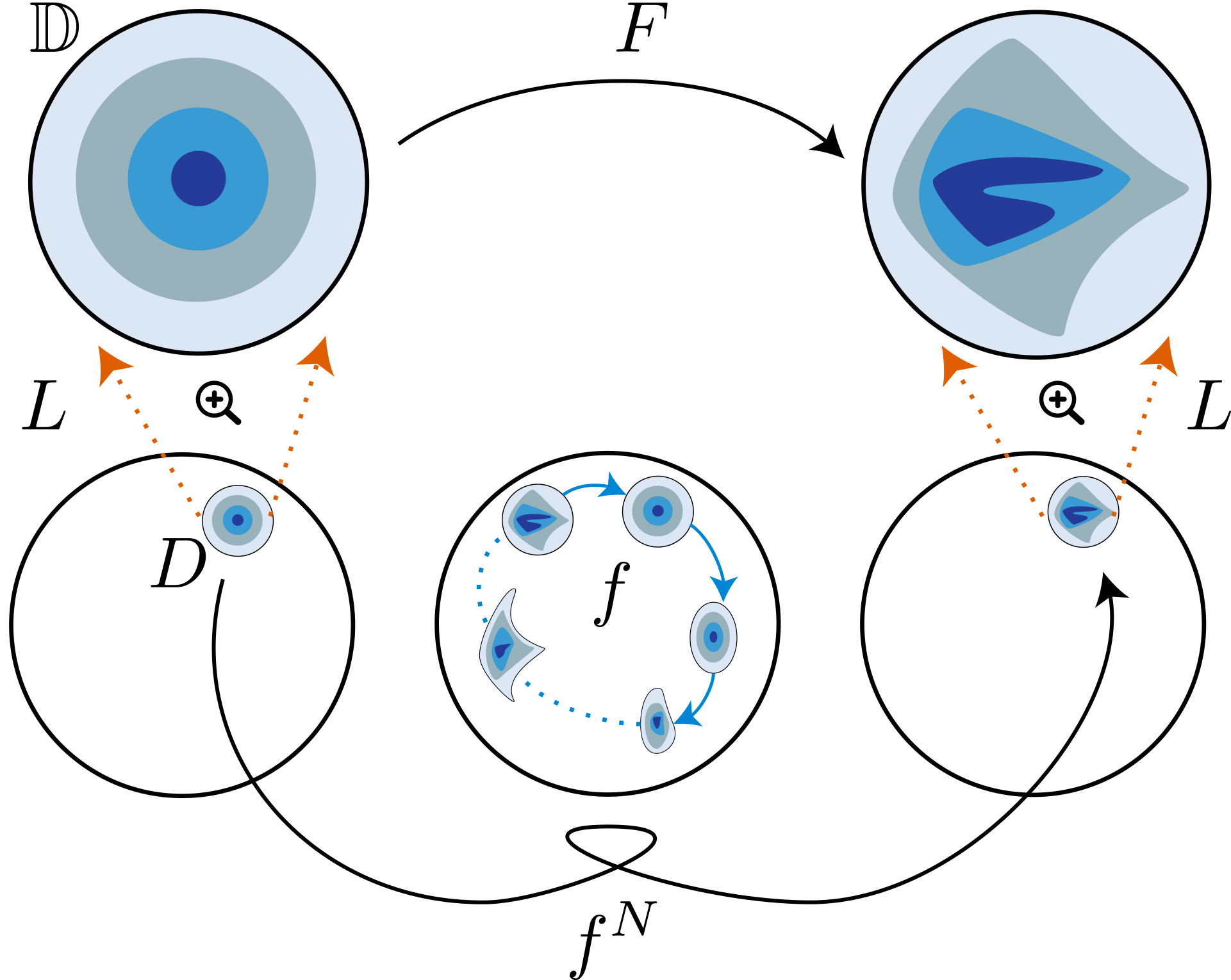
Fig. 1 : On retrouve la dynamique de F dans celle de f en itérant et en zoomant.
Alors la loupe envoie l’orbite par fN de tout point dans D sur une orbite de F. Réciproquement toute orbite de F correspond a une orbite de fN. Ainsi la complexité dynamique de f est au moins proportionnelle à celle de F. On dit que F est une renormalisation de f. Notons que F ne décrit pas entièrement la dynamique de f, car cette dernière peut avoir des orbites qui ne rencontrent pas D.
Pour obtenir une renormalisation qui voit toutes les orbites, les auteurs considèrent les dynamiques sur les espaces ayant un cercle en facteur, par exemple l’anneau M = 𝕊1 × [0,1] (leur résultat s’applique aussi en toute dimension supérieur à 2). Ils montrent que tout difféomorphisme F d’un tel espace est une renormalisation totale d’un difféomorphisme f proche de l’identité : toutes les orbites rencontrent le domaine D.
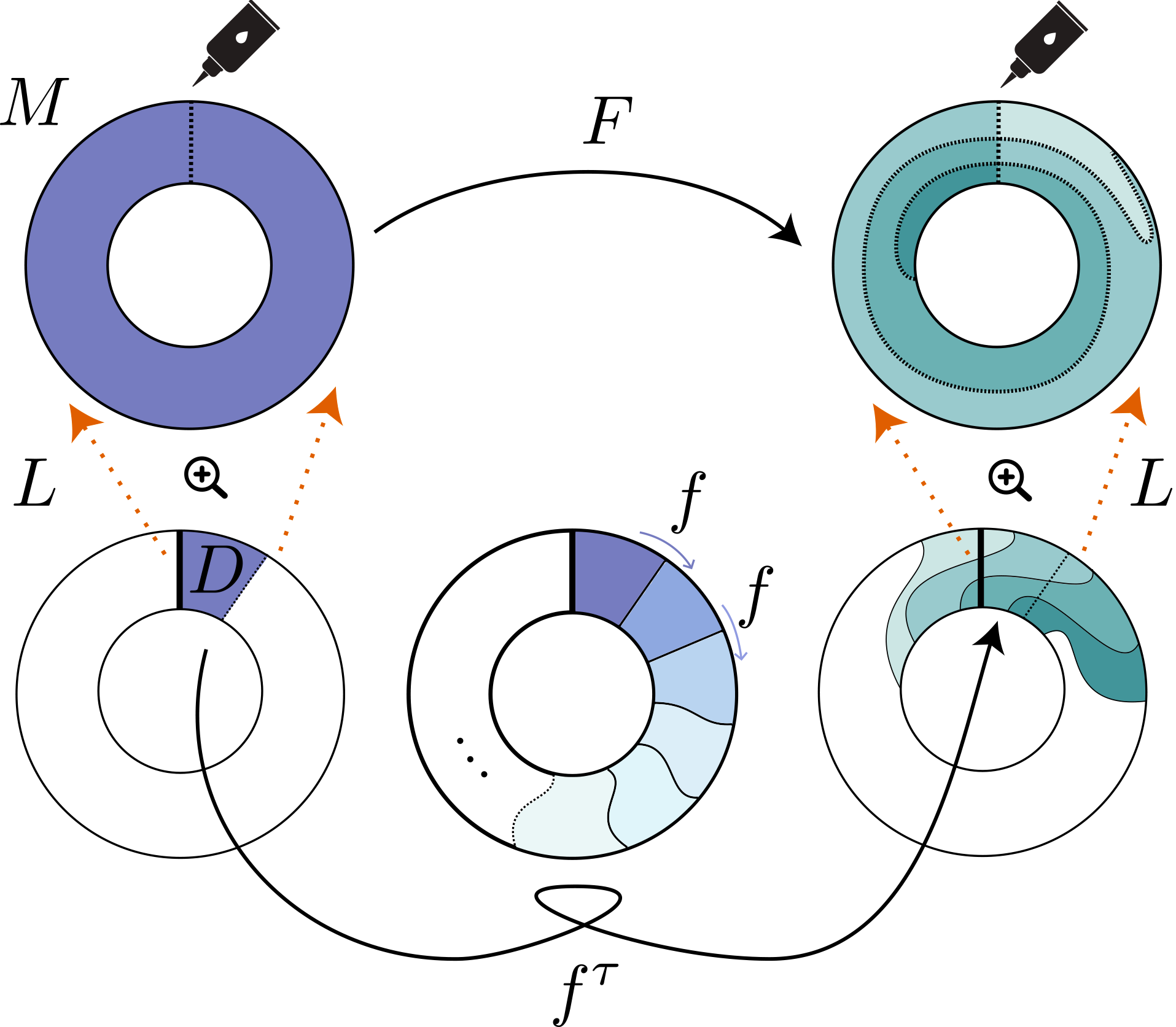
Fig. 2 : Le domaine rectangulaire D de l’anneau M = 𝕊1 × [0,1] rencontre toutes les orbites de f. La loupe L étire D jusqu’à ce que ses côtés gauche et droit se rejoignent, de façon à recouvrir entièrement M.
Pour ce faire, ils demandent à la loupe L : D → M, non plus d’être un difféomorphisme, mais seulement d’être infiniment dérivable et bijective, comme l’illustre la figure 2. La loupe n’observe alors plus une itération fN de f, mais le premier retour fτ de f dans le domaine D, le temps τ de premier retour n’est en général pas constant sur D. On a alors :
F ∘ L = L ∘ fτ.
La preuve des auteurs consiste à introduire une classe a priori particulière de difféomorphismes qui sont des renormalisations totales de difféomorphismes proches de l’identité. Ils montrent que l’ensemble de ces difféomorphismes possède une structure de groupe de Lie (de dimension infinie). Ils peuvent alors étudier l’algèbre de Lie de ce groupe, et en utilisant des constructions d’analyse fonctionnelle, ils montrent qu’il s’agit en fait du groupe de tous les difféomorphismes.