Représenter et compter les corps de nombres

 1. Corps de nombres

On note $Q$ le corps des nombres rationnels. Un corps de nombres est un corps $K$ de caractéristique nulle et de dimension finie en tant que $Q$-espace vectoriel. On note $n$ et on appelle degré de $K$ cette dimension. Le seul corps de nombres de degré $1$ est $Q$ lui-même. Un autre corps de nombres familier est l'ensemble

$$Q (i) = \{a+bi \,  | a, b \in Q\}\subset C$$ des nombres complexes à coordonnées rationnelles. Son degré est $2$. Une $Q$-base de $Q (i)$ est $(1,i)$. Dans cette base la loi de multiplication prend une forme simple $$(a+bi)(a'+b'i)=aa'-bb'+(ab'+a'b)i.$$

Ce n'est pas le seul corps de nombres de degré $2$. Par exemple l'ensemble

$$Q(\sqrt 5)=\{a+b\sqrt 5 \,  | a, b \in Q\}\subset R$$ des nombres réels de la forme $a+b\sqrt 5$ avec $a$ et $b$ rationnels est lui-aussi un corps de nombres de degré $2$. La loi de multiplication dans la $Q$-base $(1,\sqrt 5)$ est $$(a+b\sqrt 5)(a'+b'\sqrt 5)=aa'+5bb'+(ab'+a'b)\sqrt 5.$$ Tout élément d'un corps de nombres $K$ de degré $n$ est racine d'un polynôme à coefficients rationnels  de degré $\leqslant n$. On distingue les éléments de $K$ qui sont racines d'un polynôme unitaire à coefficients dans l'anneau $Z$ des entiers. On les nomme entiers algébriques de $K$. Ils forment un sous-anneau de $K$ noté $O$. Ce sous-anneau est un $Z$-module libre de rang $n$, le degré de $K$. Par exemple les entiers algébriques dans $Q (i)$ sont les $a+bi$ avec $a$ et $b$ dans $Z$. Dans le corps de nombres $Q (\sqrt 5)$ tous les nombres de la forme $a+b\sqrt 5$ avec $a$ et $b$ dans $Z$ sont des entiers algébriques, mais ce ne sont pas les seuls. Le nombre d'or $\alpha = (1+\sqrt 5)/2$ est entier lui aussi car il est racine du polynôme $x^2-x-1$. Le entiers de $Q (\sqrt 5)$ sont les $a+b\alpha$ avec $a$ et $b$ dans $Z$.

L'espace de Minkowski associé à un corps de nombres $K$ est le produit tensoriel

$$M = K\otimes_Q R.$$ Il existe deux entiers $r\geqslant 0$ et $s\geqslant 0$ tels que $r+2s=n$ et $M$ est isomorphe au $R$-espace vectoriel $R^r\oplus C^s$. L'entier $r$ est le nombre d'homomorphismes injectifs $\rho$ du corps $K$ dans le corps $R$ des nombres réels. On dit que $K$ a $r$ plongements réels. L'entier $s$ est le nombre d'homomorphismes injectifs $\sigma$ du corps $K$ dans le corps $C$ des nombres complexes, qui ne sont pas des plongements réels, divisé par deux (car on ne distingue pas $\sigma$ du plongement obtenu en composant $\sigma$ avec la conjugaison complexe). On dit que $K$ a $2s$ plongements complexes. On écrit $$M \simeq \bigoplus_{\rho} R \oplus \bigoplus_\sigma C$$ où l'indice $\rho$ parcourt l'ensemble des plongements réels et $\sigma$ parcourt un ensemble de représentants des paires de plongements complexes conjugués.

Cette décomposition permet de munir $M$ d'un produit scalaire noté $<,>$. Par exemple si $K=Q(\sqrt 5)$ on a $r=2$ et $s=0$ et

$$<a+b\sqrt 5,a'+b'\sqrt 5>= (a+b\sqrt 5)(a'+b'\sqrt 5) +(a-b\sqrt 5)(a'-b'\sqrt 5)=2aa'+10bb'.$$ et si $K=Q(i)$ on a $r=0$ et $s=1$ et $$<a+bi,a'+b'i> = (a+bi)\overline{(a'+b'i)}+ \overline{(a+bi)}(a'+b'i)$$ donc $$<a+bi,a'+b'i> = (a+bi)(a'-b'i)+(a-bi)(a'+b'i)$$ puis $$<a+bi,a'+b'i> = 2aa'+2bb'.$$ On obtient de la même manière une norme $L^2$ et une norme $L^\infty$ sur $M$. Le corps $K$ et l'anneau des entiers $O$ s'injectent canoniquement dans l'espace de Minkowski. Le $Z$-module $O$ est ainsi réalisé comme sous-groupe additif discret de $M$. Et le quotient $M/O$ est compact. Le volume de ce quotient pour la forme volume associée au produit scalaire $<,>$ est appelé covolume de $O$. C'est un invariant important du corps de nombres. Concrètement, si $\alpha_1$, ..., $\alpha_n$ est une $Z$-base de $O$ et si l'on note $\tau_1$, ..., $\tau_n$ les $n$ plongements (réels ou complexes) de $K$ alors on définit la  matrice $$A= (\tau_j(\alpha_i))_{1\leqslant i, j\leqslant n}.$$ Le covolume de $O$ est le module du déterminant de $A$.
Par exemple pour $K =Q(i)$ on obtient $$A =\begin{pmatrix}1&1\\i&-i \end{pmatrix} \text{ et } covol (O)=2.$$ Et pour $K =Q(\sqrt 5)$ on obtient $$A =\begin{pmatrix}1&1\\\frac{1+\sqrt 5}{2}&\frac{1-\sqrt 5}{2} \end{pmatrix} \text{ et } covol (O)=\sqrt 5.$$ Le discriminant de $K$ est le déterminant $$d_K = \det (AA^{t}).$$ C'est un nombre entier relatif. Sa valeur absolue est le carré du covolume de $O$. Par exemple, le discriminant de $Q(i)$ est $-4$ et le discriminant de $Q (\sqrt 5)$ est $5$.

Le degré $n$ et le discriminant $d_K$ sont deux invariants importants mais insuffisants : il existe des corps de nombres non-isomorphes de même degré et de même discriminant.

Les trois problèmes naturels suivants sont voisins :

• Trouver un système d'invariants d'un corps de nombres, aussi complet et aussi peu redondant que possible,
• Trouver une description (un modèle algébrique) d'un corps de nombres aussi concis que possible,
• Evaluer le nombre $N_n(H)$ de classes d'isomorphismes de corps de nombres de degré $n$ donné et de discriminant borné en valeur absolue par un entier $H$ donné.

On doit à Cohen, Diaz et Olivier des tables de corps de nombres en petits degrés
[6, 7, 8]. Ces tables suggèrent que $N_n(H)$ pourrait être équivalent à $c(n)\times H$ pour $n\geqslant 2$ fixé et $H\rightarrow +\infty$, où $c(n)$ est une fonction de $n$. C'est bien le cas pour $2\leqslant n\leqslant 5$. Le cas $n=2$ est élémentaire. Davenport et Heilbronn [10] ont étudié le cas  $n=3$ et Bhargava [4,5] les cas  $n=4, \, 5$.

Pour des valeurs arbitraires de $n$, on obtient des estimations plus ou moins grossières de $N_n(H)$ en étudiant la géométrie de l'anneau des entiers $O$, vu comme un sous-groupe discret de l'espace de Minkoswki $M$, muni du produit scalaire $<,>$. C'est l'objet de la géométrie des nombres dont il est question dans la section suivante.

Schmidt [12] a ainsi montré que $N_n(H)$ est majoré par $H^{\frac{n+2}{4}}$ multiplié par une fonction qui ne dépend que de $n$. Ellenberg and Venkatesh [11] ont montré qu'il existe une constante $C$ telle que $N_n(H)$ est majoré par $H^{\exp (C \sqrt{\log n})}$ multiplié par une fonction qui ne dépend que de $n$.

2. Le théorème de Minkowski

Soit $E$ un espace euclidien de dimension $n$. On note $<,>$ le produit scalaire. On se donne un sous-groupe discret $L$ de $E$ tel que le quotient $E/L$ soit compact : le rang du $Z$-module $L$ est égal à la dimension $n$ de $E$. On se donne une fonction de jauge

$$f : E \rightarrow [0,+\infty [$$ telle que

• $f(e)>0$ si $e\in E$ est non-nul,
• $f(\lambda e)=\lambda f(e)$ si $\lambda >0$ et $e\in E$,
• $f(e_1+e_2)\leqslant f(e_1)+f(e_2)$ si $e_1, e_2 \in E$.

Typiquement on prend pour $f$ la norme $L^\infty$ dans une base de $E$. On note

$$B = \{e\in E \, | \, f(e)\leqslant 1\}$$ la boule unité correspondante. On note $vol (B)$ le volume pour la forme volume associée au produit scalaire $<,>$ de l'ensemble convexe $B$.

Le second théorème de Minkowski affirme qu'il existe $n$ éléments $l_1$, …, $l_n$ dans $L$ qui sont linéairement indépendants et tels que

$$\prod_{1\leqslant i\leqslant n}f(l_i)\leqslant \frac{2^n \times cov ( L)}{vol (B)} .$$

Supposons que les $f_i$ sont numérotés de telle sorte que les $f(l_i)$ forment une suite croissante. Alors on déduit de l'inégalité précédente que

$$\begin{equation}\label{eq:li}       f(l_i)\leqslant  \left(\frac{2^n \times cov(L)}{vol(B)} \right)^{\frac{1}{n-i+1}}.     (1)\end{equation}$$

Cette inégalité est surtout utile pour les premières valeurs de $i$. Dans la situation qui nous intéresse $E$ est l'espace de Minkowski $M$ d'un corps de nombres et $L$ est l'anneau $O$ des entiers. On choisit pour $f$ la norme $L^\infty$ dans la base canonique de $M$. Schmidt utilise l'inégalité (1) pour montrer que $K$ est engendré, en tant que $Q$-algèbre, par un petit nombre d'entiers de petite norme. C'est ainsi qu'il obtient une majoration de $N_n(H)$.

Bhargava, Shankar, Taniguchi, Thorne, Tsimerman, et ZhaoSee ont remarqué [3] [Theorem 3.1] que l'existence sur $O$ d'une structure d'anneau intègre compatible avec la métrique induite par la fonction de jauge permet de renforcer l'inégalité (1) On peut montrer par exemple [9] [Proposition 1] qu'il existe  $n$ entiers $l_1$, …, $l_n$ dans $O$ qui sont linéairement indépendants et tels que

$$f(l_i)\leqslant \delta_K^2$$ pour tout $1\leqslant i\leqslant n$ où $$\delta_K = |d_K|^{\frac{1}{n}}$$ est appelé discriminant racine de $K$. Autrement dit, le $Q$-espace vectoriel $K$ admet une base formée d'entiers de petite norme.

Pour construire un modèle du corps de nombres $K$ il faut un système de générateurs $\kappa_1$, …, $\kappa_r$ de la $Q$-algèbre $K$. Il faut aussi décrire l'idéal des relations algébriques entre ces générateurs. Pour obtenir un modèle aussi concis que possible on choisit un petit nombre de générateurs, tous aussi petits que possible. Typiquement $r$ est de l'ordre de $\log n$. On choisit un degré $d$, de l'ordre de $\log n$ lui aussi. Et l'on étudie le $Z$-module des relations entre les monomes $\prod {1\leqslant k\leqslant r}\kappa_r^{e_r}$ de degré $\leqslant d$. On mobilise une foisencore le théorème de Minkowski pour montrer qu'il existe quelques relations de degré $\leqslant d$ avec de petits coefficients. On voudrait s'assurer que ces petites relations engendrent l'idéal des relations entre les générateurs $(\kappa_k) {1\leqslant k\leqslant r}$. C'est malheureusement très difficile. On se contentera d'un système d'équations locales. On cherche donc $r$ équations à coefficients dans $Z$ dont les différentielles soient linéairement indépendantes aux $n$ points complexes de l'espace affine $A^r(C)$ définis par les $r$-coordonnées affines $(\kappa_k) {1\leqslant k\leqslant r}$ et les $n$ plongements de $K$ dans $C$. Pour montrer l'existence de telles équations, un instrument de géométrie algébrique locale est requis. C'est le théorème d'Alexander et Hirschowitz [1,2] selon lequel les problèmes d'interpolation d'Hermite sont génériquement bien posés en degré $d\geqslant 5$. Ce théorème est brièvement introduit dans la section suivante.

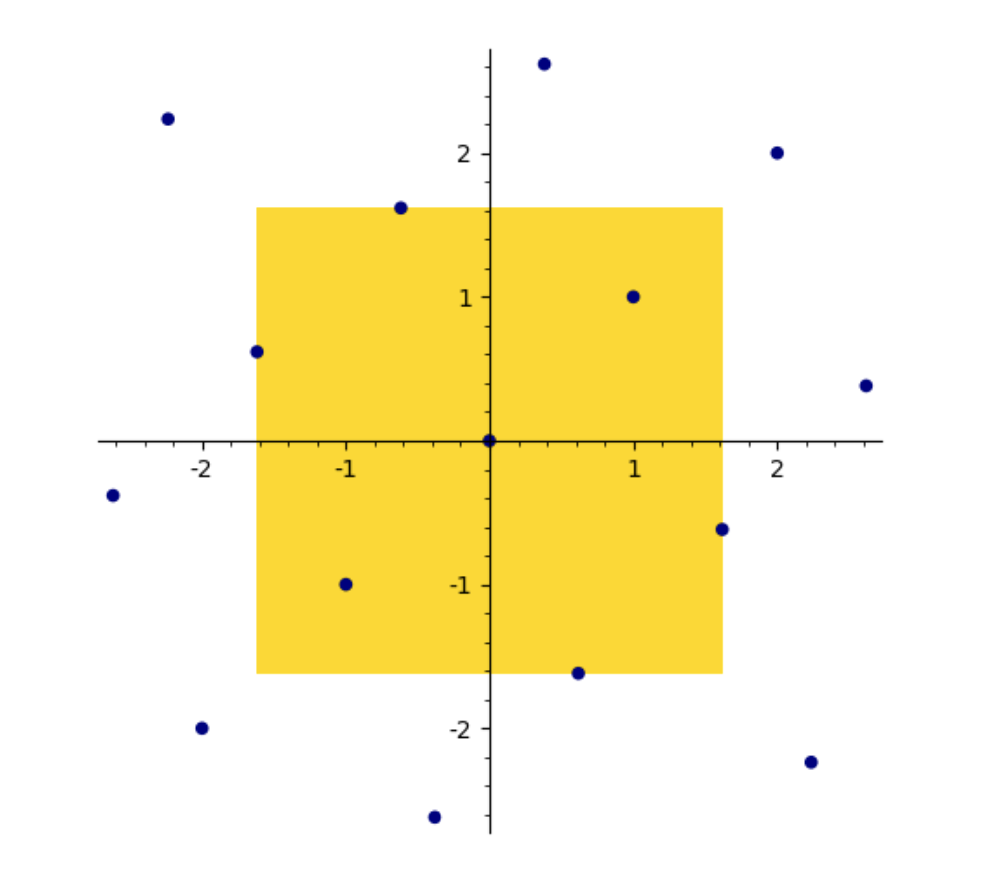
FIGURE 1. L'espace de Minkowski $M \simeq R\times R$ de $Q(\sqrt 5)$. Les points bleus sont les éléments de l'anneau $O$ des entiers. Le carré jaune est la plus petite boule $L^\infty$ qui contient deux entiers linéairement indépendants.

3. Le théorème d'Alexander et Hirschowitz pour l'interpolation multivariée

Soit $K$ un corps et $r\geqslant 1$ un entier. Soient $P_1$, $P_2$, …, $P_n$ des points dans l'espace affine $A^r(K)=K^r$. Soit $d\geqslant 1$ un entier. Etant donnée une collection $(a_i)_{1\leqslant i\leqslant n}\in K^n$ de scalaires, le problème d'interpolation de Lagrange s'intéresse à l'existence (et à l'unicité) d'un polynôme $f$ dans $K[x_1, …, x_r]$ de degré $\leqslant d$ et tel que $f(P_i)=a_i$ pour tout $1\leqslant i\leqslant n$. Comme la dimension de l'espace des polynômes de degré $\leqslant d$ en $r$ variables est ${d+r\choose r}$ on n'espère pas mieux que l'existence si $n\leqslant {d+r\choose r}$ et l'unicité si $n\geqslant {d+r\choose r}$. On dit donc que le problème d'interpolation est bien posé quand l'application d'évaluation $f\mapsto (f(P_1), …, f(P_n))$ de $K[x_1, …, x_r]_{\leqslant d}$ dans $K^n$ est injective ou surjective. Il est facile de voir que les problèmes d'interpolation de Lagrange sont génériquement bien posés. Autrement dit l'ensemble des problèmes mal posés est un fermé strict de l'ensemble $(A^r)^n$ des nuages de $n$ points dans $A^r$. Pour s'en convaincre il suffit d'écrire le déterminant d'un mineur maximal de l'application d'évaluation et de vérifier que les termes de son développement sont des monômes en $rn$ variables de multidegrés deux-à-deux distincts.

Il arrive que l'on souhaite contrôler non seulement les valeurs d'un polynôme de $K[x_1, …, x_r]$ en $n$ points, mais aussi les valeurs de ses $r$ dérivées partielles en ces $n$ points. On parle alors d'interpolation d'Hermite. Un théorème difficile d'Alexander et Hirschowitz donne la liste des triplets $(r,n,d)$ pour lesquels le problème générique d'interpolation d'Hermite est bien posé. Cette liste comporte tous les triplets tels que $d\geqslant 5$. C'est ce théorème qui permet de contrôler les équations locales des petits modèles de corps de nombres. On obtient ainsi [9] le théorème suivant.

THEOREME 1 (Petits modèles d'un corps de nombres).

Il existe une constante positive $C$ telle que ce qui suit est vrai. Soit  $K$ un corps de nombre de degré $n\geqslant C$ et de discriminant racine $\delta_K$. Il existe deux entiers $r\leqslant C \log n$ et $d\leqslant C \log n$ tels que ${d+r\choose r}\leqslant C n\log n$ et il existe $r$ polynômes  $E_1$, $E_2$, …, $E_r$ de degré  $\leqslant d$ dans $Z[x_1, …, x_r]$, ayant tous leurs coefficients bornés par  $(n\delta_K)^{C {\log n}}$ en valeur absolue, tels que la $Q$-variété affine lisse et de dimension nulle définie par les équations

$$E_1 = E_2 = … = E_r=0 \text{ et } \det \left( \partial E_i/\partial x_j \right)_{1\leqslant i, \, j\leqslant r} \not = 0$$ contienne une composante irréductible de corps résiduel $K$.

On peut résumer ce théorème en disant qu'un corps de nombres de degré $n$ et discriminant racine $\delta_K$ admet une description algébrique de \og taille \fg \, une constante fois

$$n(\log n)^3(\log \delta_K+\log n).$$

On déduit facilement de ce théorème qu'il existe une constante $D$ telle que si $n\geqslant D$ alors $N_n(H)$ est majoré par $n^{D n\log^3n}H^{D \log^3 n}$ pour tout $H$. L'exposant $\exp(C\sqrt{\log n})$ dans l'estimation de Venkatesh-Ellenberg est ainsi remplacé par un polynôme en $\log n$. On est loin encore de l'exposant $1$ suggéré par les données expérimentales.