Maths & Océans #1 : Comment localiser les baleines dans l'océan ?

C’est une question que j’ai entendue au détour d’un repas de famille bien avant de l’aborder d’un point de vue mathématique. Ma belle-mère, Corinne, adore les baleines et embarque souvent dans les croisières de deux heures en bateau qui promettent d’observer ces mammifères. Mais bien souvent, elle rentre bredouille, pestant contre les organisatrices et organisateurs qui, selon elle, « n’ont pas su trouver une baleine ».

Voilà donc ma question : existe-t-il, dans cette situation, une méthode pour estimer la position d’une baleine ? J’ai choisi aujourd’hui l’exemple des baleines, mais j’aurais aussi pu penser à un bateau de pêche cherchant un banc de poissons, ou à un navire militaire sondant l’océan pour localiser un sous-marin. Dans tous ces cas, le principe reste le même et s’appuie sur les méthodes de sonar dites passives. On équipe le bateau d’un micro sous-marin, appelé hydrophone, qui enregistre les sons se propageant dans l’eau. Lorsque l’objet recherché émet un bruit, ce bruit se propage et peut être capté par l’hydrophone.

Pour les baleines, l’un des sons les plus caractéristiques est appelé le gunshot. Il s’agit d’un claquement très net produit par la baleine et qui ressemble à un coup de feu (vous pouvez l’écouter ici). Ce son se propage particulièrement bien dans l’eau et se distingue très nettement dans les enregistrements. Nous avons donc trois éléments : une baleine qui émet un gunshot, un enregistrement de ce son depuis le bateau, et une question : comment utiliser cet enregistrement pour retrouver la distance d entre le bateau et la baleine ? 

La situation parfaite 

Commençons par le cas le plus simple, en supposant que l’on sache exactement à quel instant  la baleine a émis son gunshot. La vitesse  des ondes acoustiques dans l’eau étant connue () si le son est reçu par le bateau à l’instant , on peut alors écrire que . 

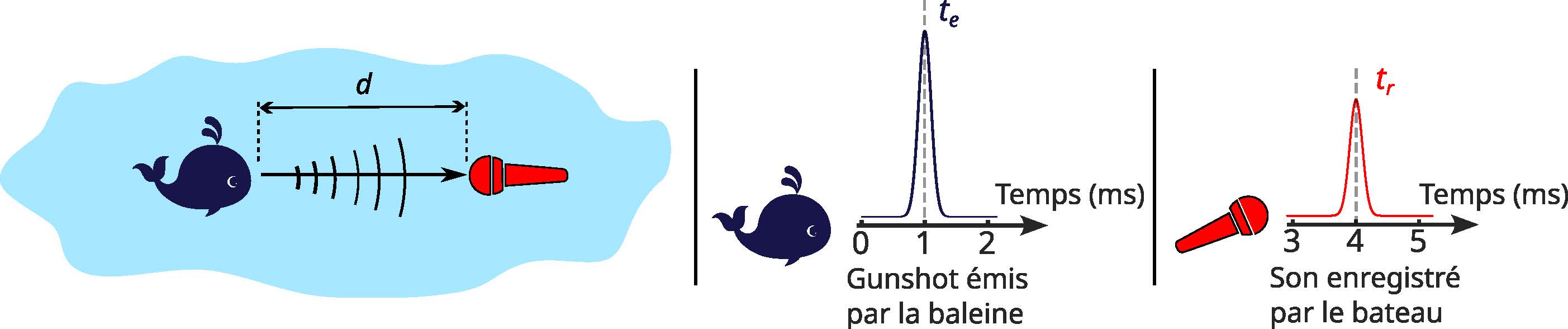
Simple… en apparence. Car deux difficultés majeures apparaissent rapidement. Vous en avez peut-être déjà identifié une : comment Corinne, depuis le bateau, pourrait-elle savoir à quel instant précis ​ la baleine a émis son gunshot ? Sans cette information, nous avons une équation mais deux inconnues, ce qui rend le problème insoluble. La seconde difficulté est plus subtile : l’océan n’est pas un milieu homogène et la propagation du son ne se fait pas seulement en ligne droite.

Les modes

En réalité, le son se propage dans toutes les directions et, lorsqu’il rencontre une interface (la surface de l’eau ou le fond marin), une partie de l’énergie acoustique repart dans l’air ou dans le sol, tandis qu’une autre reste dans l’eau. Les directions de propagation sont alors données par les lois de Snell-Descartes. 

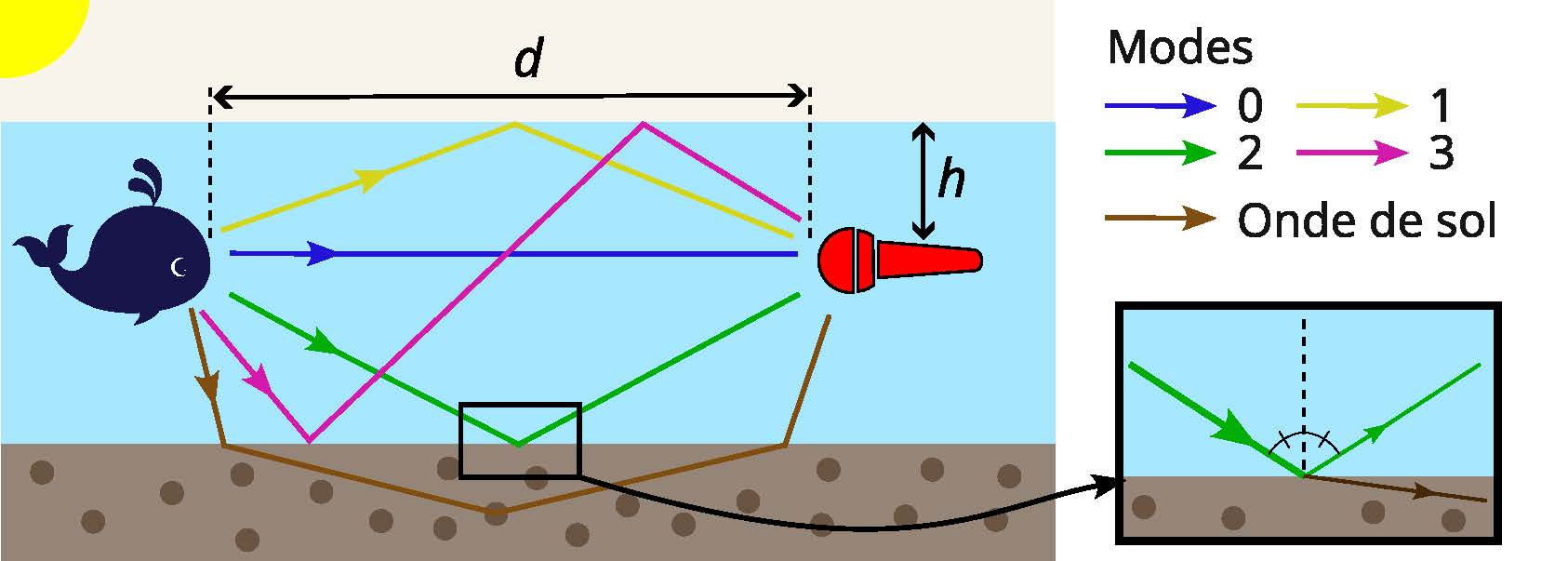
Résultat : pour aller de la baleine à l’hydrophone, l’onde peut emprunter plusieurs chemins. On parle alors de modes de propagation. Le chemin direct en ligne droite est appelé mode 0, mais le son peut aussi rebondir sur la surface (mode 1), sur le fond (mode 2), puis combiner plusieurs réflexions successives (modes 3, etc.). On peut ainsi décomposer le signal reçu comme une somme, en théorie infinie, de contributions correspondant à ces différents modes. En pratique, les réflexions successives dissipent l’énergie et au-delà de trois ou quatre, le signal devient trop faible pour être détecté.

Premier temps d’arrivée

Imaginons un instant que Corinne connaisse l’instant exact ​ de l’émission. Malgré la complexité de la propagation, on pourrait se contenter d’identifier le premier mode reçu, le mode 0, qui arrive à un instant ​, et d’appliquer la formule précédente :

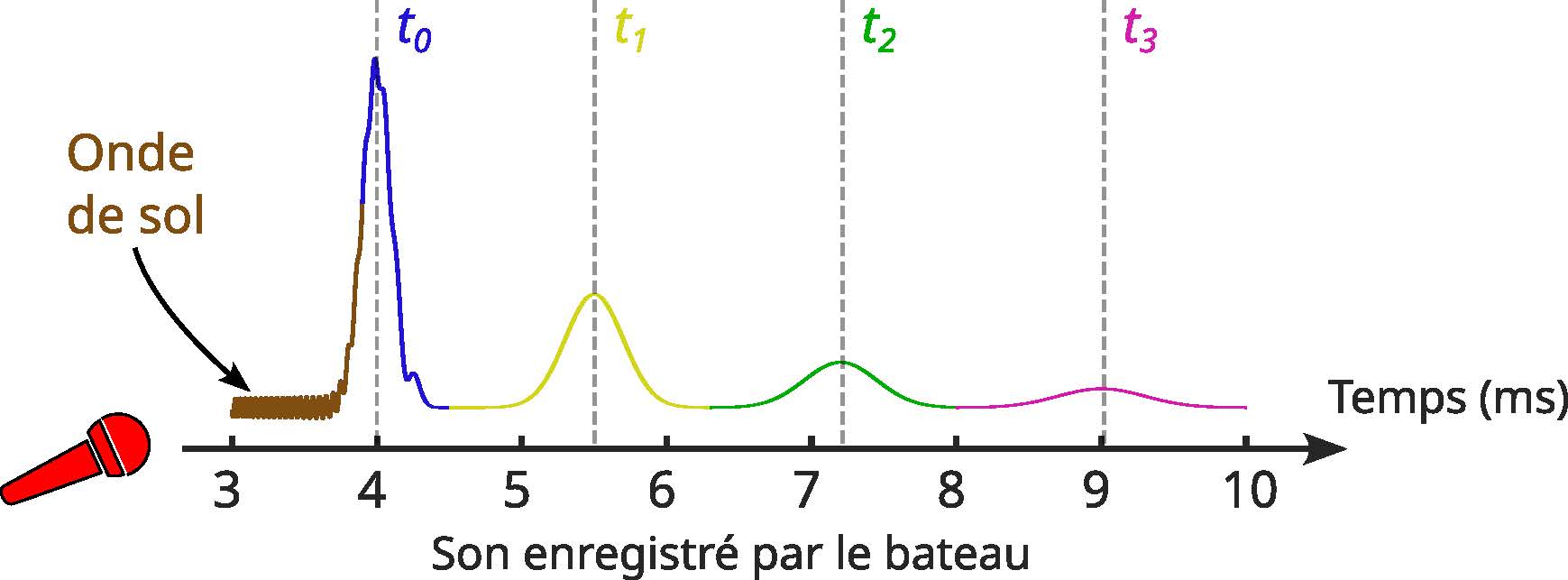
Cette approche, connue sous le nom de méthode du premier temps d’arrivée, a longtemps été utilisée dans les sonars actifs. Mais même dans cette configuration idéale, la méthode se heurte à un problème : déterminer précisément est difficile, car un bruit parasite précède presque toujours l’arrivée du mode 0. Ce bruit est en réalité dû à un mode particulier, l’onde de sol, qui se propage dans les sédiments du fond marin plus rapidement que dans l’eau, et qui réapparaît juste avant le mode 0.

Idée générale 

Et puis, dans notre situation réelle, le temps d’émission est de toute façon inconnu. Voyez-vous comment nous en sortir ? Un indice : utilisez les autres modes ! Si j’ai présenté la propagation complexe des ondes dans l’océan comme un inconvénient, c’est en réalité un atout : cette complexité nous fournit de nombreuses informations exploitables. En mesurant non seulement , mais aussi , le temps d’arrivée du mode 1, nous obtenons deux équations portant sur deux inconnues ( et ). En supposant que la baleine et le micro sont à mètres de la surface, seriez-vous capables de trouver ces deux équations ? En utilisant nos souvenirs de géométrie, on trouve en fait que 

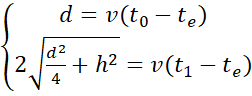
puis en soustrayant les équations que . 

Il ne reste plus qu’une équation à une inconnue. Certes, elle n’est pas triviale à résoudre, mais une calculatrice ou un ordinateur le fait sans difficulté, et si dans notre exemple et avec les temps issus de la figure 3, il pourra indiquer que .

Augmenter les inconnues 

Mais… Et si Corinne ne connaît pas la profondeur de la baleine ? Encore une nouvelle inconnue !  Il suffit alors d’ajouter un troisième temps d’arrivée, par exemple . On dispose alors de trois équations à trois inconnues. Et si la vitesse des ondes dans l’eau est incertaine, on peut aussi tenir compte de , ce qui fournit quatre équations pour quatre inconnues. On devine le principe : plus on mesure de modes, plus on peut estimer de paramètres. 

Bien sûr, la description que je donne ici est très simplifiée. Dans la réalité, les signaux reçus ne sont pas de simples impulsions, et les relations reliant les temps d’arrivées des modes​ aux paramètres physiques sont plus complexes (vous pouvez malgré tout aller voir les équations 4 et 5 pour vous faire une idée). Mais l’idée générale est bien celle-ci : d’abord formuler le problème direct, c’est-à-dire relier les paramètres physiques (, , …) aux temps d’arrivée () puis résoudre le problème inverse, qui consiste à chercher les paramètres qui reproduisent au mieux les observations, même si les équations n’ont pas de solution exacte.

Les applications sont multiples. Outre le plaisir d’offrir à Corinne l’assurance de voir une baleine, ces méthodes non invasives (puisqu’elles se contentent d’écouter les sons de l’océan) permettent d’étudier les déplacements et le comportement d’espèces marines menacées, afin de mieux les protéger. Elles peuvent aussi servir à suivre l’évolution des océans dans le contexte du réchauffement climatique : la température de l’eau influe directement sur la vitesse des ondes acoustiques, et donc sur les temps d’arrivée mesurés. De ce fait, à partir d’enregistrements destinés initialement à détecter des baleines ou des bancs de poissons, il est souvent possible d’extraire aussi des informations sur la température locale de l’eau. Ces données sont faciles et peu coûteuses à collecter : n’importe quel bateau équipé d’un hydrophone peut en enregistrer des milliers. Enfin, comme la vitesse des ondes dans le sol marin intervient elle aussi dans les équations, ces enregistrements permettent également d’en apprendre davantage sur la nature du fond, ouvrant la voie à des méthodes d’imagerie sous-marine économiques.

En résumé, localiser une baleine à partir d’un son, ce n’est pas seulement mesurer une distance : c’est aussi accéder, indirectement, à la profondeur, à la température et même à la composition du fond marin. De quoi transformer chaque croisière en expédition scientifique… et donner à Corinne une bonne raison de sourire à son retour.